3.3 Projections and Least Squares
- TOC {:toc}
이 글은 KOCW의 한양대학교 선형대수 ‘11강 벡터투영과 최소제곱법’ 및 ‘12강 1차연립방정식 풀이와 직교벡터 구하기’ 강의내용을 복습하기 위해 Gilbert Strang의 Linear Algebra and Its Applications 3.3장과 강의노트를 기반으로 작성한 글입니다.
- 제가 필요한 부분 위주로 확인하면서 정리하고 있어 글에 덜 작성된 부분이 있을 수 있습니다.
- 글 작성 후 원 서적의 내용이 수정되거나 내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있습니다. 되도록 원 서적을 참고해주시길 바랍니다.
- 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
미지수(unknown)보다 식(equation)의 수가 더 많은 경우 대부분 solution이 존재하지 않는다: Overconstrained cases
Example
$$ \begin{matrix} 2x &=& b_1 \ 3x &=& b_2 \ 4x &=& b_3 \end{matrix}
\quad \rightarrow \quad
\begin{bmatrix} 2 \ 3 \ 4 \end{bmatrix} x = \begin{bmatrix} b_1 \ b_2 \ b_3 \end{bmatrix} $$
Solution이 존재하는 경우는 $b$가 $C(A)$안에 있는 경우로 매우 드물다.
$$ b= \begin{bmatrix} b_1 \ b_2 \ b_3 \end{bmatrix} \in C(A) \rightarrow
b\ \text{is multiple of}
\ a = \begin{bmatrix} 2 \ 3 \ 4 \end{bmatrix} $$
Solution은 $x={b_1/2}={b_2/3=b_3/4}$
대부분의 경우 정확한 solution은 구할 수 없지만 column space $C(A)$안에 존재하는 vector중 가장 적합한 vector를 찾을 수 있다 → Least Squares
Optimal Solution : Least Squares
평균 오차(average error) $E$를 최소화 시키는 vector $x$를 구하는 것이 system의 optimal solution과 같다.
평균을 구하는 가장 보편적인 방법은 각 항목의 제곱(square)을 더하는 것으로 위의 system에 적용해보면
$$ E^2 = (2x-b_1)^2 = (3x-b_2)^2 + (4x-b_3)^3 $$
이는 $x$에 대한 이차방정식이므로 미분값이 0이 되는 지점이 최소값으로 error가 최소가 되는 지점이다.
$$ {{dE^2} \over {dx}} = 2[(2x-b_1)2+(3x-b_2)3+(4x-b_3)4] = 0 $$
$$ \hat{x} = {2b_1+3b_2+4b_3 \over 2^2 + 3^2 + 4^2} = {a^Tb \over a^Ta} $$
보다 일반적인 경우,
$$ E^2 = \lVert ax-b \lVert^2 = (ax_1-b_1)^2 + \cdots + (ax_m-b_m)^2 $$
$E^2$가 0이 되는 point $\hat{x}$는: $$ (a_1\hat{x}-b_1)a_1 + \cdots + (a_m\hat{x}-b_m)a_m = 0 $$ $$ \hat{x} = {a_1b_1 + \cdots a_mb_m \over a_1^2 + \cdots + a_m^2} = {a^Tb \over a^Ta} $$
미지수가 한 개인 system $ax=b$의 least-square solution은 line $a$에 projection한 결과와 같다.
Orthogonality of $a$ and $e$
least square problem을 기하학적으로 해석하면 결국 $b$와 $a$의 거리를 최소화하는 것이고 이전 단원에서와 동일하게 $b$와 $p$를 잇는 error vector $e$가 $a$에 수직이어야 한다.
$$ a^T(b-\hat{x}a)=a^T-{a^Tb \over a^Ta}a^Ta = 0 $$
Least Squares Problems with Several Variables
전 단원에서 line에 한정지었던 projection을 space로 확장. → Matrix $A$가 m by n matrix. column의 수가 1개가 아닌 $n$개
그 외는 이전과 동일하다.
- $m>n$으로 inconsistent
- $b$는 $C(A)$ 밖에 있다. $A$의 column vector의 combination으로 나타낼 수 없다.
- 핵심은 오차를 최소화하는 vector $\hat{x}$를 찾는 것
오차는 $E=\lVert Ax-b \lVert$로 $b$와 column space 안의 $Ax$ 사이의 거리이다.
least-square solution $\hat{x}$를 찾기 위해서는 $b$에 가장 가까운 $p=A\hat{x}$를 구해야 하고 이는 $b$를 column space에 projection 시킨 point 이다.
그렇다면 error vector $e=b-A\hat{x}$가 column space에 수직이므로 이를 이용해서 $\hat{x}$와 $p=A\hat{x}$를 다음과 같은 방법으로 구할 수 있다.
- column space와 수직인 모든 벡터는 left nullspace안에 있으므로 $e=b-A\hat{x}$는 $A^T$의 nullspace 안에 있다. $$ A^T(b-A\hat{x})=0 \quad or \quad A^TA\hat{x}=A^Tb $$
- error vector $e$가 각 column vector $a$에 orthogonal하다. $$ a_i^T(b-A\hat{x}) = 0 \rightarrow \begin{bmatrix} a_1^T \ \vdots \ a_n^T \end{bmatrix} \begin{bmatrix} \quad \ b-A\hat{x} \ \quad \end{bmatrix} = \begin{bmatrix} 0 \ \vdots \ 0 \end{bmatrix} $$ $$ A^T[b-A\hat{x}] = 0 \quad or \quad A^TA\hat{x}=A^Tb $$
- Calculus way $$ E^2 = \lVert Ax-b \lVert^2 = (Ax-b)^T(Ax-b) $$ $$ {dE^2 \over dx} = A^T(Ax-b) + (Ax-b)A^T = 2A^TAx - 2A^Tb = 0 $$ $$ A^TAx = A^Tb $$
공통적으로 나온 식은 $Ax=b$ 양변에 $A^T$를 곱한 $A^TA\hat{x} = A^Tb$으로 normal equations 라고 한다.
$A$의 column이 모두 linearly independent하면 $A^TA$가 invertible 하고 정확한 $\hat{x}$를 구할 수 있다.
- $\text{Best estimate: }\hat{x} = (A^TA)^{-1}A^Tb$
$b$를 column space로 projection한 $p$는
- $\text{Projection: }p = A\hat{x} = A(A^TA)^{-1}A^Tb$
Example
$$ A= \begin{bmatrix} 1 & 2 \ 1 & 3 \ 0 & 0 \end{bmatrix} , \quad b= \begin{bmatrix} 4 \ 5 \ 6 \end{bmatrix}, \quad
Ax=b \ \text{has no solution} $$
우선 별도의 계산 없이,
- $A$의 마지막 항이 모두 0이므로 column space는 $R^3$에서 x-y plane이다.
- $b = (4, 5, 6)$는 공간상에 놓인 한 점이므로
- 이를 x-y plane에 projection하면 $p=(4, 5, 0)$이다.
Normal equation을 풀어서 확인해보면 $$ \begin{aligned}
A^TA &= \begin{bmatrix} 1 & 1 & 0 \ 2 & 3 & 0 \end{bmatrix} \begin{bmatrix} 1 & 2 \ 1 & 3 \ 0 & 0 \end{bmatrix} = \begin{bmatrix} 2 & 5 \ 5 & 13 \end{bmatrix} \ \
\hat{x} = (A^TA)^{-1}A^Tb &= \begin{bmatrix} 13 & -5 \ -5 & 2 \end{bmatrix} \begin{bmatrix} 1 & 1 & 0 \ 2 & 3 & 0 \end{bmatrix} \begin{bmatrix} 4 \ 5 \ 6 \end{bmatrix} = \begin{bmatrix} 2 \ 1 \end{bmatrix} \ \
p = A\hat{x} &= \begin{bmatrix} 1 & 2 \ 1 & 3 \ 0 & 0 \end{bmatrix} \begin{bmatrix} 2 \ 1 \end{bmatrix} = \begin{bmatrix} 4 \ 5 \ 0 \end{bmatrix}
\end{aligned} $$
$A$는 위의 matrix가 아니더라도 x-y plane을 구성할 수만 있으면 되기 때문에 계산이 간단한 matrix로 잡는 것이 편하다. e.g $\begin{bmatrix} 1 & 0 \ 0 & 1 \ 0 & 0\end{bmatrix}$
Remarks
Remarks 1
$b$가 이미 $A$의 column space안에 있는 vector라면 ($Ax=b$) $b$를 projection한 결과는 여전히 $b$이다.
$b\ \text{in column space}$
- $p = A(A^TA)^{-1}A^Tb = A(A^TA)^{-1}A^TAx = Ax = b$
Remarks 2
정반대의 경우로 $b$가 column space의 모든 column에 수직인 vector이면 ($A^Tb = 0) $b$는 zero다. vector로 projection한다.
$b\ \text{in left nullspace}$
- $p = A(A^TA)^{-1}A^Tb = a(A^TA)^{-1}0 = 0$
Remarks 3
일련의 실험을 진행해서input $t$에 대한 linear function의 결과로 output $b$가 나오는 일련의 실험을 진행했다고 가정하자.$A$가 square matrix이고 invertible 하면 column space는 whole space이다. 모든 vector는 자기 자신으로 project한다. $p$는 $b$와 같고 $\hat{x}=x$이다.
$\text{If A is invertible}$
- $p=A(A^TA)^{-1}A^Tb = AA^{-1}(A^T)^{-1}A^Tb = b$
The Cross-Product Matrix $A^TA$
$A^TA$는 symmetric하다.
$$ (A^TA)^T = A^TA^TT = A^TA $$
문제는 $A$가 invertible하냐는 것이다. 다행히:
$A^TA$는 $A$와 같은 nullspace를 갖는다.
proof
- $Ax = 0$ 이면 $A^TAx = 0$이다.
- 반대 방향으로도 성립하는지 보기 위해 $A^TAx = 0$이라고 가정한 뒤 $x$를 내적하면
$ x^TA^TAx = 0, \quad or \quad \lVert Ax \lVert^2 = 0, \quad or \quad Ax = 0 $
$A$가 independent columns를 가지면 $A^TA$는 $\text{square, symmetric}$ and $\text{invertible}$ 하다.
Projection Matrices
위에서 $b$에 가장 가까운 point $p$를 나타내는 식이 $p=A(A^TA)^{-1}A^Tb$임을 밝혔다.
이 식은 $b$에서 $A$의 column space로 수직인 line을 내리는 matrix를 나타낸다.
$$ \text{Projection matrix} \quad P=A(A^TA)^{-1}A^T $$
- Matrix $P$는 임의의 vector $b$를 $A$의 column space로 project한다. $$p = pb \in C(A)$$
- 그 외의 component는 $C(A)$에 orthogonal하다. 즉, $A$의 left nullspace 안에 있다. $$ e=b-Pb \in N(A^T) $$
Projection matrix $P=A(A^TA)^{-1}A^T$는 기본적으로 두 성질을 갖는다.
- $\text{It equals its square: }P^2=P$
- $\text{It equals its transpose: }P^T=P$
Proof
$P^2=P$
임의의 $b$에서 시작하더라도 $Pb$는 우리가 project하는 subspace안에 놓이게 된다. 이를 다시 project하더라도 $Pb$는 이미 subspace안에 존재하기 때문에 변하는 것이 없고 $P(Pb)$는 여전히 $Pb$이다.
$$ P^2 = A(A^TA)^{-1}A^TA(A^TA)^{-1}A^T = A(A^TA)^{-1}A^T = P $$
$P^T=P$
$P$의 transpose를 취해서 (A^TA)^{-1}의 symmetry를 이용해 역순으로 곱해나가면 $P$로 돌아오게된다.
$$ P^T = (A^T)^T((A^TA)^{-1})^TA^T = A(A^TA)^{-1}A^T = P $$
반대로, $P^2=P$와 $P^T=P$로부터 $Pb$가 $b$를 $P$의 column space로 projection하는 것이라는 것을 알아낼 수 있다.
$b-Pb$는 space에 orthogonal하기 때문에 space안의 임의의 vector $Pc$와 내적하면 그 값은 0이다. $$ (b-Pb)^TPc = b^T(I-P)^TPc = b^T(P-P^2)c = 0 $$ 그러므로 $b-Pb$가 space에 orthogonal하면 $Pb$는 column space로 projection한 것과 같다
Example $A$를 invertible한 4 by 4 matirx이고 네 개의 column이 모두 independent하다고 하면 column space는 whole space인 $R^4$이다.
Whole space인 $A$로 projection하는 matrix는 identity matrix이다.
$$ P = A(A^TA)^{-1}A^T = AA^{-1}(A^T)^{-1}A^T = I $$
Identity matrix는 symmetric하고 $I^2=I$이며 error $b-Ib$는 zero다.
Least-Squares Fitting of Data
Input $t$에 대한 linear function의 결과로 output $b$가 나오는 일련의 실험을 진행했다고 가정하자.
이 때, 실험 결과를 나타내는 $\text{straight line }b=C+Dt$를 찾으려한다.
만약 실험오차가 없다면 $b$의 두 결과값을 골라 $C, D$를 찾을 수 있겠지만, 그렇지 않다면 optimal line을 찾기 위해 실험결과의 “평균”을 찾아야한다.
$$ \begin{matrix} C + Dt_1 = b_1 \ C + Dt_2 = b_2 \ \vdots \ C + Dt_m = b_m \end{matrix} $$
이는 2개의 미지수와 m개의 equation이 있는 overdetermined system이기 때문에 오차가 있다면 solution이 존재하지 않는다.
$$ \begin{bmatrix} 1 & t_1 \ 1 & t_2 \ \vdots & \vdots \ 1 & t_m \end{bmatrix} \begin{bmatrix} C \ D \end{bmatrix} =
\begin{bmatrix} b_1 \ b_2 \ \vdots \ b_m \end{bmatrix}, \quad or \quad Ax = b $$
Best solution $\hat{x} = (\hat{C}, \hat{D})$는 squared error $E^2$를 최소화하는 $x$이다.
이 때 error는 straight line으로 까지의 $\text{Vertical distance } b-C-Dt$이다. 즉, 이 값들을 제곱한 뒤 더해서 최소가 되는 $b$를 구하는 것이라고 할 수 있다.
$$ \text{Minimize} \quad E^2 = \lVert b-Ax \lVert^2 = (b_1-C-Dt_1)^2 + \cdots + (b_m-C-Dt_m)^2 $$
Example (12강 일차 연립방정식의 풀이 부분)
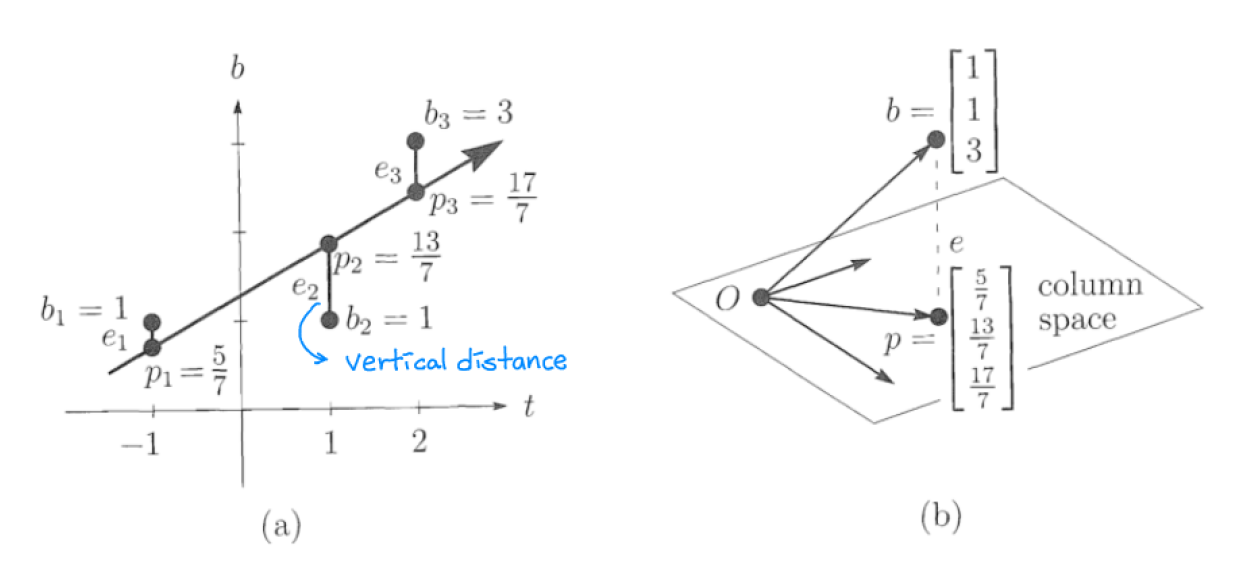
측정값 $(b,t)$ 세 개가 각각 $(1, -1), (1, 1), (3, 2)$ 일때,
세 point를 모두 지나는 line을 가정해서 equation을 적으면, $$ Ax = b \quad is \quad \begin{matrix} C &-& D &=& 1 \ C &+& D &=& 1 \ C &+& 2D &=& 3 \end{matrix} \quad or \quad \begin{bmatrix} 1 & -1 \ 1 & 1 \ 1 & 2 \end{bmatrix} \begin{bmatrix} C \ D \end{bmatrix} = \begin{bmatrix} 1 \ 1 \ 3 \end{bmatrix} $$
세 포인트는 하나의 line에 놓여있지 않으므로 $Ax=b$는 least square을 이용해서 풀어야 한다.
$$ A^TA\hat{x} = A^Tb \quad is \quad \begin{bmatrix} 3 & 2 \ 2 & 6 \end{bmatrix} \begin{bmatrix} \hat{C} \ \hat{D} \end{bmatrix} = \begin{bmatrix} 5 \ 6 \end{bmatrix} $$
$\hat{C}={9 \over 7}, \hat{D}={4 \over 7}$이므로 best line은 ${9 \over 7} + {4 \over 7}t$
이 문제를 line과 space 두 관점으로 볼 수 있다.
예시에서 세 point는 하나의 line위에 존재하지 않는다. 즉 Figure b에서와 같이 $b$는 $(1,1,1)$과 $(-1,1,2)$의 combination(plane)에 존재하지 않는다.
이를 해결하기 위해서는 least squares로 line위에 있지 않은 point $b$를 line위에 있는 point $p$로 바꾼다.
Fitting한 line은 -1, 1, 2 지점에서 각각 $5 \over 7$, $13 \over 7$, $17 \over 7$의 값을 갖는다. 그러므로 column space의 $p=($5 \over 7$, $13 \over 7$, $17 \over 7$)이다. 그리고 이 vector는 $b$를 column space로 projetion한 vector다.
$p$에서 $b$를 뺀 error $e=({2 \over 7}, -{6 \over 7}, {4 \over 7})$은 line의 vertical error 값과 같다. $e$ vector는 A의 첫 columne과 두 번쨰 column에 모두 orthogonal하므로 ($e \perp C(A)$) $A$의 left nullspace에 놓여있다.
straight line에 fitting 하기 위한 equation을 정리하면
임의의 각 point $t_1, \cdots, t_m$에 대한 측정값이 $b_1, \cdots, b_m$일 때 에러 $E^2$를 최소화 시키는 line $\hat{C}+\hat{D}t$는
$$ A^TA \begin{bmatrix} \hat{C} \ \hat{D} \end{bmatrix} = A^Tb \qquad or \qquad \begin{bmatrix} 1 & \cdots & 1 \ t_1 & \cdots & t_n \ \end{bmatrix} \begin{bmatrix} 1 & t_1 \ \vdots & \vdots \ 1 & t_n \end{bmatrix} \begin{bmatrix} \hat{C} \ \hat{D} \end{bmatrix} = \begin{bmatrix} m & \Sigma t_i \ \Sigma t_i & \Sigma t_i^2 \end{bmatrix} \begin{bmatrix} \hat{C} \ \hat{D} \end{bmatrix} = \begin{bmatrix} \Sigma b_i \ \Sigma t_ib_i \end{bmatrix} $$
Weighted Least Squares
13강 일반 최소제곱법 부분. 자세하게는 다루지 않음.
Generalized least square
$x_i$마다 발생할 확률인 weight $(w_i)$을 부여한다.
$$ \begin{matrix} E^2 &=& w_1^2(x-b_1)^2 + w_2^2(x-b_2)^2 \
\hat{x}_i &=& {w_1^2b_1+w_2^2b_2 \over w_1^2+w_2^2} \end{matrix} $$
$$ \begin{matrix} WAx &=& Wb \ A^TW^TWAx &=& A^TW^TWb \end{matrix} \quad \text{W: weight matrix} $$
-
draft