3.1 Orthogonal Vectors and Subspaces
- TOC {:toc}
이 글은 KOCW의 한양대학교 선형대수 ‘10강 벡터의 직교성과 직선투영’ 강의내용을 복습하기 위해 Gilbert Strang의 Linear Algebra and Its Applications 3.1장과 강의노트를 기반으로 작성한 글입니다.
- 제가 필요한 부분 위주로 확인하면서 정리하고 있어 글에 덜 작성된 부분이 있을 수 있습니다.
- 글 작성 후 원 서적의 내용이 수정되거나 내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있습니다. 되도록 원 서적을 참고해주시길 바랍니다.
- 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
Orthogonality
- 기하학적으로 생각하면 basis는 space를 이루는 coordinate axes로 볼 수 있다.
- 일반적으로 봐왔던 x-y plane이나 3-dimensional space의 axes처럼 수직을(perpendicular) 이루고 있는 basis를 orthogonal하다고 한다.
- Orthogonal한 basis로 계산을 보다 쉽게 할 수있다.
Orthogonal Vectors
그럼 어떤 vector가 orthogonal한 벡터일까.
두 벡터 $x$, $y$가 orthogonal한지 확인하려면 가장 먼저 vector의 길이를 알이야한다.
Length of Vector
Vector x의 길이(lentgh)는 $\lVert x \lVert$로 나타내고 그 제곱을 다음과 같이 나타낼 수 있다.
$$ \lVert x \lVert^2 = \sum_{i=1}^n {x_i}^2 = x^Tx \quad (x^Tx: inner product) $$
Orthogonal vectors
orthogonal한 두 basis vector $x$, $y$는 right triangle을 형성하고 삼각형 각 변을 이루는 vector의 크기를 피타고라스 정리를 이용해서 표현하면 다음과 같다.
$$ \lVert x \lVert^2 + \lVert y \lVert^2 = \lVert {x - y} \lVert^2 $$
위 식의 vector 크기를 내적을 이용해서 나타내면
$ \begin{matrix} x^Tx + y^Ty &=& {(x-y)}^T(x-y) \ &=& x^Tx - y^Tx - x^Ty + y^Ty \end{matrix} $
$x^Ty + y^Tx = 0$
vector $x$와 $y$를 내적한 값은 scalar값이므로 transpose를 취해도 그 값이 같다.
즉, $x^Ty = (x^Ty)^T = y^Tx$ 이므로
$x^Ty = y^Tx = 0$ 이다.
$x^Ty$의 값이 zero이면 $x$와 $y$는 orthogonal 하다.
$x^Ty$ is zero if and only if $x$ and $y$ are orthogonal vectors.
$x$와 $y$를 내적할 때
- $x^Ty = 0$ for Orthogonal (right angle)
- $x^Ty < 0$ for angle > $90\degree$
- $x^Ty > 0$ for angle < $90\degree$
Orthogonality and Linearly Independent
nonzero vercor $v_1, v_2 \cdots, v_k$가 mutually orthogonal하면 (모든 verctor가 서로 수직) 이 vectors들은 linearly independent하다.
Proof
$c_1v_1 + c_2v_2 + \cdots + c_kv_k = 0$일 때,
임의의 $v_i$에 대해 ${v_i}^T(c_1v_1 + c_2v_2 + \cdots + c_kv_k) = {v_i}^T \cdot 0 = c_i\lVert {v_i} \lVert^2 = 0$
$\because \ v_iv_j = 0 \ (i \neq j)$
nonzero $v_i$에 대해 $c_i\lVert {v_i} \lVert^2 \neq 0$ 이므로 모든 $c_i = 0$
Orthonormal
Basis vector $v_1, v_2 \cdots, v_k$가 orthogonal 하면서 $v_i$의 length가 $\lVert {v_i} \lVert=1$ 일 때 vector $v_i$는 orthonornal 하다.
Orthonormal한 basis vector $v_1, v_2 \cdots, v_k$가 이루는 vector space $V$안의 임의의 벡터 $x$에 대해서 $x$는 $v_i$의 linear combination으로 나타낼 수 있다.
$$ x = \sum_{i=1}^k c_iv_i $$
이 때, Basis vector가 orthonormal하면 linear coefficient $c_i$를 보다 쉽게 구할 수 있다.
$v_i \cdot x = c_i \lVert v_i \lVert^2$
for orthonormal $v_i$, $\lVert v_i \lVert^2=1$
$c_i = v_i \cdot x$
Orthogonal Subspaces
동일한 space $R$의 두 개의 subspace $V$와 $W$에 대해서 $V$의 모든 vector $v$가 $W$의 모든 vector $w$에 orthogonal하면 두 subspace $V$와 $W$는 orthogonal하다. $v^Tw = 0$ for all $v$ and $w$.
- {0}는 모든 subspace에 orthogonal하다.
- $R^3$의 subspace는 원점을 지나는 line(1-dimension)이나 plane(2-dimension)으로 나타낼 수 있으며 line과 line 혹은 line과 plane 사이에 orthogonality가 성립할 수 있다.
Orthogonal Subspace in Four Fundamental Subspace
- 어떤 Space의 orthogonal subspace는 항상 두 개가 동시에 존재한다*.
- 그리고 fundamental subspaces가 orthogonal subspace를 이루기 때문에 orthogonal subspace는 항상 존재한다 (unavoidable).
* 생각해보면 subspace가 ‘수직’을 이루려면 당연히 두 개가 존재해야한다.
m by n matrix에 $A$에 대해서,
Row space는 $R^n$에서 nullspace와 orthogonal 하다.
Column space는 $R^m$애서 left nullspace와 orthogonal 하다.
proof 1
nullspace의 vector $x$에 대해서 $Ax=0$ 이고 이 system의 m개의 equation을 다음과 같이 표현할 수 있다.
$$ Ax= \begin{bmatrix} \quad row\ 1 \quad \ row\ 2 \ \vdots \ row\ m \end{bmatrix}
\begin{bmatrix} x_1 \ x_2 \ \vdots \ x_n \end{bmatrix}
= \begin{bmatrix} 0 \ 0 \ \vdots \ 0 \end{bmatrix} $$
A의 각 row는 $x$와 orthogonal하기 떄문에 $x$는 rows의 어떤 combination이라도 orthogonal하다. $(row)^T \cdot x = 0$
Nullspace의 vector x는 모든 row space의 vector에 orthogonal하므로 nullspace는 row space에 orthogonal하다. $N(A) \perp C(A^T)$
Left nullspace의 vector $y$ 역시 $A^Ty = 0$ 혹은 $y^TA = 0$ 이고 이 system을 다음과 같이 나타닐 수 있다.
$$ y^TA= \begin{bmatrix} y_1 & \cdots & y_m \end{bmatrix}
\begin{bmatrix} c & & c \ o & & o \ l & & l \ u & \cdots & u \ m & & m \ n & & n \ \ 1 & & n \end{bmatrix}
= \begin{bmatrix} 0 & \cdots & 0 \end{bmatrix} $$
Vector $y$는 모든 column에 orthogonal 하므로 column의 모든 combination에 orthogonal하다.
Left nullspace의 vector $y$는 column space의 모든 vector에 orthogonal하므로 left nullspace는 column space에 orthogonal하다. $N(A^T) \perp C(A)$
Proof 2 coordinate-free proof
$x$가 $Ax = 0$를 만족하는 nullspace일 때 $v$가 row space의 vector라면 $v$는 A의 row들의 combination으로 나타낼 수 있다. $v = A^Tz$ ($z$는 coefficients).
이 경우 $x$와 $v$는 다음을 만족한다.
$$ v^T = (A^Tz)^Tx = z^TAx = z^T0 = 0 $$
Null space $\perp$ Row space
Example
Rank가 1인 matrix A에 대해서
$$ A= \begin{bmatrix} 1 & 3 \ 2 & 6 \ 3 & 9 \end{bmatrix} $$
- row는 $(1, 3$의 상수배이기 때문에 nullspace는 $A$의 모든 row에 orthogonal한 $x = (3, -1)$를 포함한다.
- nullspace와 row space는 $R^2$ 안의 수직한 line이다.
- column space는 $(1, 2, 3)$을 지나는 line이므로 left nullspace는 그에 수직인 plane인 $y_1 + 2y_2 + 3y_3 = 0$이다.
Orthogonal Complement
위의 예시에서 처음 두 개의 sub spaces (two lines)는 $R^2$안에서 $1+1=2$의 dimension을 갖는다. 두 번쨰 sub spaces (line and plane)는 $R^3$안에서 $1+2=3$의 dimension을 갖는다.
이를 일반적으로 적용하면,
- dimension of (row space) + (nullspace) = $r + (n-r) = n$ (number of columns) in $R^n$
- dimension of (column space) +(left nullspace) = $r + (m-r) = m$ (number of rows) in $R^m$
이 처럼 subspace 사이에 orthogonal 하면서 dimension에 보완 관계가 있는 경우 orthogonal complement라고 한다.
$R^n$의 sub space $V$에 대해서 $V$에 orthogonal한 모든 vector를 $V$의 orthogonal complement라고 하고 $V^{\perp} = V$ perp 라고 표시한다.
- row space $\perp$ nullspace: $C(A^T) = (N(A))^{\perp}$
- column space $\perp$ left nullspace: $C(A) = (N(A^T))^{\perp}$
결과적으로 four fundamental subspaces의 관계를 정리하면 다음과 같다.
- nullspace는 $R^n$에서 row space의 orthogonal complement이며 row space의 vector에 orthogonal한 모든 vector를 포함한다.
- left nullspace는 $R^m$에서 column space의 orthogonal complement이며 column space의 vector에 orthogonal한 모든 vector를 포함한다.
Ax = b
Column space와 left nullspace의 orthogonal complement를 이루는 성질을 $Ax = b$에 이용할 수 있다.
- $Ax = b$의 solution이 존재하기 위해서는 $b$가 $A$의 column space에 있어야 한다. ($b$가 column space의 linear combination)
- 즉 $b$가 $A$의 left nullspace에 perpendicular 해야한다.
$Ax = b$는 $y^TA=0$ 일 때, $y^Tb = 0$이면 해가 존재한다.
$Ax = b$ is solvable if and only if $y^Tb = 0$ whenever $y^TA = 0$
The Matrix and the Subspaces
Orthogonal complement와 orthogonal은 다르다.
dimension이 작은 경우 orthogonal하지만 orthogonal complement는 아닐 수 있다.
Example
$V$가 (0, 1, 0)이 span한 line이고 $W$가 (0, 0, 1)이 span한 line인 경우, $V$와 $W$는 orthogonal하지만 $V$가 $W^\perp$는 아니다.
$W$의 orthogonal complement는 2-dimensional한 plane이어야 하고 위의 line은 $W^\perp$의 일부분일 뿐이다.
Dimension이 충분하면(right) orthogonal sub space들은 무조건 orthogonal complement를 이룬다.
$W=V^\perp$ 이면 $V=W^\perp$ 이고 $dim\ V + dim\ W = n$ 이다.
즉, $V^{\perp\perp} = V$ 이고 이는 $V$와 $W$의 dimension이 충분하면 whole space $R^n$은 두 개의 수직한 부분으로 나눠진다는 것을 의미한다.
Summary of Fundamental Theorem of Linear Algebra
What is happening inside the multiplication $Ax$
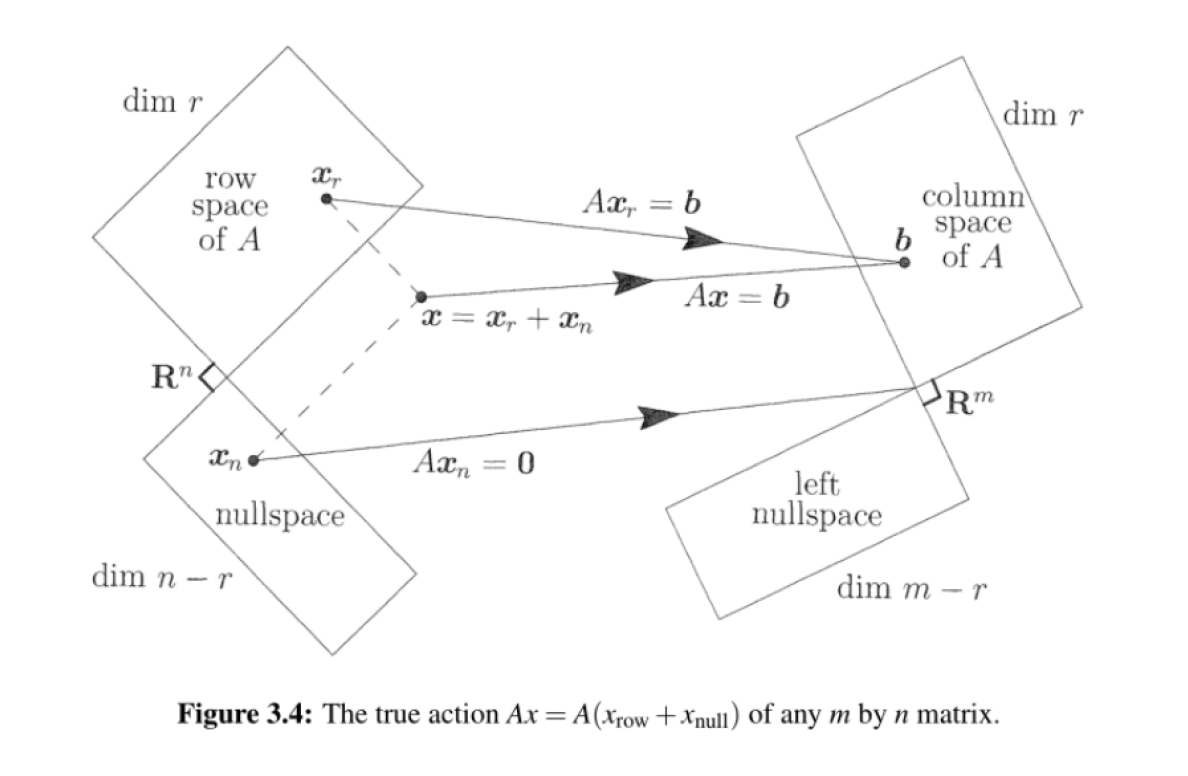
- Nullspace는 zero vector로 이동.
- 모든 $Ax$는 $A$의 column space안에 존재.
- 그 어느 것도 left nullspace로는 이동하지 않음.
일반적으로 $x$는 “row space compoment”와 “null space component”로 나눌 수 있다. $x = x_r + x_n$
- $x$에 $A$를 곱하면, $Ax = Ax_r + Ax_n$
- Nullspace component는 zero로 간다: $Ax_n = 0$
- Row space component는 column space로 간다: $Ax_r = Ax$
$x_r$은 $x$를 row space로, $x_n$은 $x$를 nullspace로 projection한 것이다 → Projections
Transpose, Pseudoinverse
추후에 작성
3.2 Cosines and Projections onto Lines
- Vector의 inner product를 vector가 이루는 각과 연결시키기 위함.
- Vector가 이루는 각이 right angle이 아니고 그 inner product 값도 zero가 아닌 경우.
Projection
Vector $b$의 point에서 $a$방향으로 향하는 가장 직선 거리.
- Line $a$의 위에 있는 point 중 $b$와 가장 가까운 point $p$를 찾으면
- $b$와 $p$를 연결하는 직선은 $a$에 수직이다.

Line이 아니라 plane이나 임의의 subspace $S$가 주어져도 상황은 동일하다.
point $p$는 $b$를 subspace로 projection한 것이다.
기하학적으로 projection은 point $b$와 subspace $S$의 거리와 같지만, Linear system에서는 overdetermined system의 least-squares solution을 구하는데 사용할 수 있다.
즉, $Ax = b$의 solution이 없는 경우, projection을 이용해서 least-squares method로 구한 $p$가 가장 근접하게 $b$를 대체할 수 있다.
Inner Products and Cosines
Inner product는 각이 아니지만 각의 cosine값은 inner product와 직결된다.
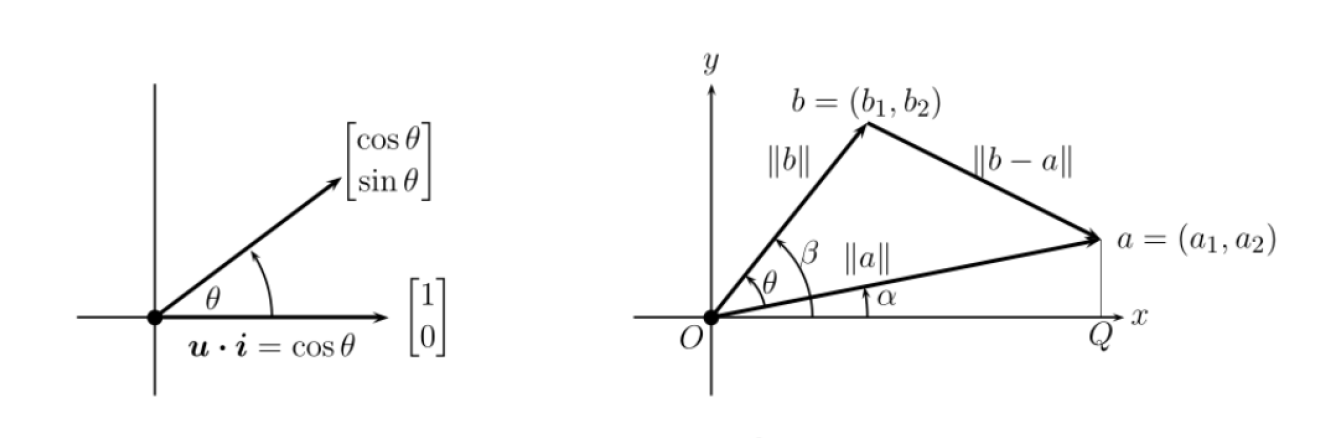
위의 그림에서 $cos\theta$는 다음과 같다.
$$ cos\theta = {{a^Tb} \over {\lVert a \lVert \lVert b \lVert}} $$
벡터를 삼각형으로 보고 law of cosines를 이용해도 동일한 결과를 구할 수 있다.
$$ Law\ of\ Cosines \quad {\lVert {b-a} \lVert}^2 = \lVert b \lVert^2 + \lVert a \lVert^2 -2\lVert b \lVert \lVert a \lVert cos\theta $$
vector의 length를 모두 inner product로 바꿔서 식을 정리하면 $$ \begin{matrix} {\lVert {b-a} \lVert}^2 &=& \lVert b \lVert^2 + \lVert a \lVert^2 -2\lVert b \lVert \lVert a \lVert cos\theta \ (b-a)^T(b-a) &=& b^Tb + a^Ta - 2\lVert b \lVert \lVert a \lVert cos\theta \ a^Tb + b^Ta &=& 2\lVert a \lVert \lVert b \lVert cos \theta \ \end{matrix} $$
$a^Tb = b^Ta$ 이므로 동일한 $cos\theta$ 값을 구할 수 있다.
Projection onto a Line
Projection point $p$를 구해보자.
$p$는 주어진 vector $a$를 이용해서 나타낼 수 있다: $p = \hat{x}a$
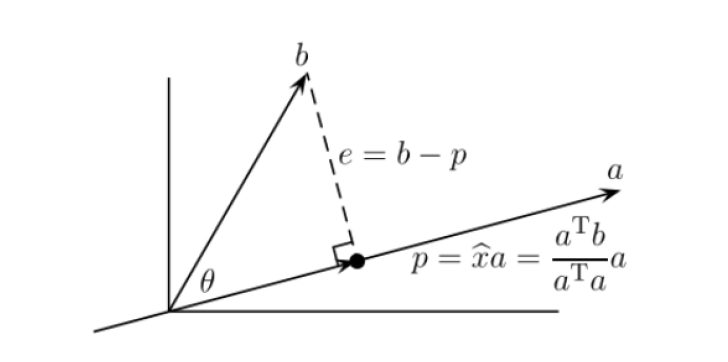
point $b$에서 $p$로의 line은 vector $a$와 수직하므로
$$ (b-\hat{x}a) \perp a, \quad or \quad a^T(b-\hat{x}a) = 0, \quad or \quad \hat{x}={a^Tb \over a^Ta} $$
를 이용해서 $\hat{x}$를 구할 수 있다.
projection onto a line $p$를 구하면
$$ p = \hat{x}a = {a^Tb \over a^Ta}a $$
Schwarz inequality
projection식을 이용해서 Schewarz inequality를 이끌어낼 수 있다.
위의 Figure에서 $\lVert e \lVert^2 = \lVert b-p \lVert^2$가 음수가 될 수 없음을 이용하면,
$$ \lVert b-{a^Tb \over a^Ta}a \lVert^2 = b^Tb-2{(a^Ta)^2 \over a^Ta} + ({a^Tb \over a^Ta})^2 a^Ta = {(b^Tb)(a^Ta) - (a^Tb)^2 \over (a^Ta)} \ge 0 $$
이로부터 $(b^Tb)(a^Ta) \ge (a^Tb)^2$임을 알 수 있다.
모든 vector $a$와 $b$는 $R^n$에서 $\vert cos\theta \vert \le 1$인 Schwarz inequality를 만족한다.
$\vert a^Tb \vert \le \lVert a\lVert \lVert b \lVert$
Example
$b=(1,2,3)$을 $a=(1,1,1)$를 지나는 line으로 projection해서 $\hat{x}$와 $p$를 구함.
$$ \hat{x} = {a^Tb \over a^Ta} = {6 \over 3} = 2, \quad p = \hat{x}a = (2,2,2) $$
$a$와 $b$사이의 각도는
$$ cos\theta = {a^Tb \over \lVert a \lVert \lVert b \lVert} = {6 \over \sqrt{3}\sqrt{14}} $$
$6 \le \sqrt{3}\sqrt{14}$로 Schwarz ineqality를 만족한다.
Projection Matrix of Rank 1
이전에 표기하던 $p = \hat{x}a$에 약간의 변화를 줘서 표기해볼 수 있다: $p=a(a^Tb/a^Ta)$
이처럼 $\hat{x}$와 $a$의 순서를 바꾸면 line으로의 projection을 Proejction matrix $P$ 를 이용해서 나타낼 수 있다. $P$는 vector $b$와 곱해져서 $p$를 만드는 matrix이다.
$$ p = a{a^Tb \over a^Ta} = {aa^T \over a^Ta}b, \quad P = {aa^T \over a^Ta} $$
Example
$a=(1,1,1)$을 지나는 line으로 project하는 matrix
$$ P = {aa^T \over a^Ta} = {1 \over 3} \begin{bmatrix} 1 \ 1 \ 1\ \end{bmatrix} \begin{bmatrix} 1 & 1 & 1 \end{bmatrix} = \begin{bmatrix} {1 \over 3} & {1 \over 3} & {1 \over 3} \ {1 \over 3} & {1 \over 3} & {1 \over 3} \ {1 \over 3} & {1 \over 3} & {1 \over 3} \end{bmatrix} $$
예시에서 두 가지 성질을 발견할 수 있다.
- $P$는 symmetric matrix이다
- Matrix를 제곱하면 자기 자신이 나온다. $P^2 = P$
$b$를 두 번 projection 하면 $P^2b$로 나타낼 수 있고 이는 $Pb$를 projection하는 것과 같다. $Pb$는 이미 line위에 있으므로 $P^2b = Pb$이다.
Projection matrix를 나타내는 식으로 계산해도 동일한 결과를 얻을 수 있다.
$$ P^2 = {(aa^T)(aa^T) \over (a^Ta)(a^Ta)} = {a(a^Ta)a^T \over (a^Ta)(a^Ta)} = {aa^T \over a^Ta} = P $$
$P$를 four fundamental subspaces의 관점에서 볼 수도 있다. 위의 예시에서 $P$는:
- $a=(1,1,1)$을 지나는 line으로 이루어진 column space
- $a$에 수직인 plane으로 이루어진 nullspace 이고
- rank $r=1$이다.
$b$ satisfying $Pb = 0$
$p=0$으로 project하는 $b$를 별도로 다뤄보면: $Pb = 0$
$P$의 모든 column이 $a$의 multiple이므로 $p=0$로 project하는 $b$는 $a^Tb=0$을 만족한다. 이는 $p=0$으로 project하는 $b$는 $a$의 nullspace (=perpendicular plane)에 놓여있다는 것을 의미한다: $b \perp a$
Remark on Scaling
Projection matrix는 scaling에 영향을 받지 않는다.
위의 예시에서 $a$를 double해도 결과는 같다.
$$ a = \begin{bmatrix} 2 \ 2 \ 2 \end{bmatrix}, \quad P = {aa^T \over a^Ta} = {1 \over 12} \begin{bmatrix} 2 \ 2 \ 2\ \end{bmatrix} \begin{bmatrix} 2 & 2 & 2 \end{bmatrix} = \begin{bmatrix} {1 \over 3} & {1 \over 3} & {1 \over 3} \ {1 \over 3} & {1 \over 3} & {1 \over 3} \ {1 \over 3} & {1 \over 3} & {1 \over 3} \end{bmatrix} $$
Example: Project onto $\theta$-line
$a=(cos\theta, sin\theta)$으로 project하는 projection matrix를 구해보면
$$ P = {aa^T \over a^Ta} = {\begin{bmatrix} c \ s \end{bmatrix} \begin{bmatrix} c & s \end{bmatrix} \over \begin{bmatrix} c & s \end{bmatrix} \begin{bmatrix} c \ s \end{bmatrix}} = \begin{bmatrix} c^2 & cs \ cs & s^2 \end{bmatrix} $$
- $c = cos\theta$ , $s=sin\theta$
- 분모의 $c^2 + s^2 = 1$
Transposes from Inner Products
Transpose는 matrix의 diagonal을 기준으로 reflection 시킨 것이다: $A^T_{ij} = (A)_{ji}$
Transpose를 inner product랑 연결시키면 transpose에 대한 좀 더 추상적(abstract)한 정의를 얻을 수 있다:
$Ax$와 $y$를 inner product한 것은 $x$와 $A^Ty를$ inner product한 것과 같다.
$$(Ax)^Ty = x^Ta^Ty = x^T(A^Ty)$$
동일한 방법으로 $(AB)^T=B^TA^T$ 역시 보일 수 있다.
$$ (Ax)^Ty = x^TA^Ty = x^T(A^Ty) $$
2020.05.04 16:05 작성.
-
draft