2.6 Linear Transformations
- TOC {:toc}
이 글은 KOCW의 한양대학교 선형대수 ‘9강 선형변환과 행렬’ 강의내용을 복습하기 위해 Gilbert Strang의 Linear Algebra and Its Applications 2.6장과 강의노트를 기반으로 작성한 글입니다.
- 제가 필요한 부분 위주로 확인하면서 정리하고 있어 글에 덜 작성된 부분이 있을 수 있습니다.
- 글 작성 후 원 서적의 내용이 수정되거나 내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있습니다. 되도록 원 서적을 참고해주시길 바랍니다.
- 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
Ax = b를 보는 여러가지 관점
- System equation. x는 solution.
- b는 A의 column vectors의 linear combination. x는 linear combination의 coefficient.
- x가 A system에 의해 b로 변환(transform)됨 $\leftarrow$ New!
임의의 m x n matrix A가 있을 때 $Ax = b$는 A를 통해 n차원의 vector x를 m차원의 vector b로 transform 시키는 것으로 볼 수 있다.
이 때 $A(a_1x_1+a_2x_2)=a_1Ax_1+a_2Ax_2$를 만족하므로 linear transform 이다.
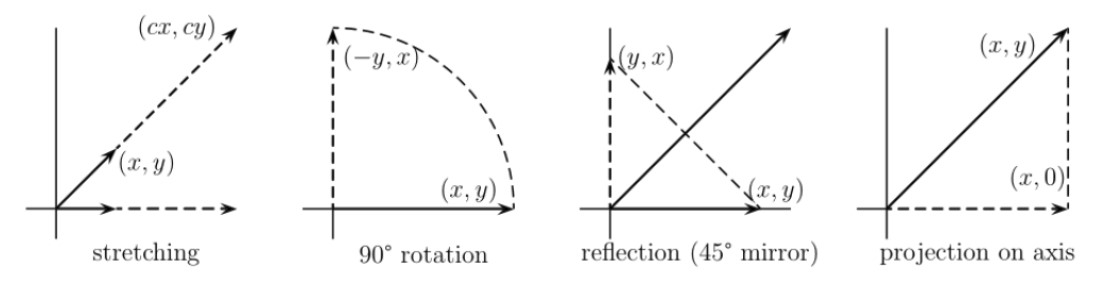
Examples
-
$A=\begin{bmatrix} c & 0 \ 0 & c \end{bmatrix}$ : stretching
-
$A=\begin{bmatrix} 0 & -1 \ 1 & 0 \end{bmatrix}$ : 90$\degree$ rotation
-
$A=\begin{bmatrix} 0 & 1 \ 1 & c \end{bmatrix}$ : Reflection by y=x
-
$A=\begin{bmatrix} 1 & 0 \ 0 & 0 \end{bmatrix}$ : projection onto x
Linear Transformation
Linear transform $T(x)=Ax$는 다음을 만족해야한다.
- 원점(Origin)은 옮길 수 없다. $A\cdot0=0$ for every matrix
모든 숫자 $c$, $d$, 모든 벡터 $x$, $y$에 대해서 linear transform은 다음을 만족한다. $$A(cx+dy)=c(Ax)+d(Ay)$$
이는 모든 matrix는 linear transformation으로 이어지는 것을 의미하고 반대로 모든 linear transformation 역시 matrix로 나타낼 수 있다.
변환이 일어나는 vector은 같은 차원일 필요가 없고, $R^n$의 vector가 $R^m$의 vector로 변환될 수도 있다. 이는 m x n matrix A에 의해 일어나는 transformation과 같다.
Example
Space $P_n$안의 degree가 n인 polynomial vector $P(t)=a_0+a_1t+a_2t^2+ \cdots + a_nt^n$을 이용하여 예시를 들어보자. $P_n$의 dimension은 $n+1$이다.
Example 1 Differentiation $A=d/dt$ $$ Ap(t) = {d \over dt}(a_0+a_1t+a_2t^2+ \cdots + a_nt^n_0) = a_1+ \cdots + na_nt^{n-1} $$
- $P_{n}$에서 $P_{n-1}$으로의 linear transformation
- $Ap(t)=0$을 만족하는 $p(t)$는 $p(t)=a_0$이므로 A의 nullspace는 1-dimentional
Example 2 Integration from 0 to t $$ Ap(t) = \int_{0}^{t} (a_0+a_1t+a_2t^2+ \cdots + a_nt^n_0), dt = a_0t + \cdots + {a_n \over n+1}t^{n+1} $$
- $P_{n}$에서 $P_{n+1}$로의 linear transformation
- Nullspace는 0외에 존재하지 않는다. $Ap(t)=0$ only if $p(t)=0$
Example 3 Multiplication by a polynomial $A=x(t)p(t)$ $$ Ap(t) = (2+3t)(a_0+a_1t+a_2t^2+ \cdots + a_nt^n_0) = 2a_0+ \cdots + 3a_nt^{n+1} $$
- $P_n$에서 $P_{n+1}$으로의 linear transformation
- Nullspace는 0외에 존재하지 않는다.
Transform Represented by Matrices
모든 basis vector에 대해서 $Ax$를 알면, 모든 vector space에 대해 $Ax$를 알 수 있다.
이는 Lineary system에서 A를 정확히 모르더라도 A를 통해 모든 basis vector를 변환한 결과를 알고 있으면 space내의 모든 vector의 변환 결과를 알 수 있다는 것을 의미한다.
How to find A?
Elementary basis vector*를 A로 변환한 vector를 column으로 하는 matrix이다.
$ x_1=\begin{bmatrix} 1 \ 0 \ \vdots \ 0 \end{bmatrix}, \quad x_2=\begin{bmatrix} 0 \ 1 \ \vdots \ 0 \end{bmatrix}, \quad x_x=\begin{bmatrix} 0 \ 0 \ \vdots \ 1 \end{bmatrix} $
$ a_1=Ax_1, a_2=Ax_1, \cdots, a_n=Ax_n, \quad A=\begin{bmatrix} a_1 a_2 \cdots a_n \end{bmatrix} $
* 강의에서 임의로 정한 명칭
Example 4 다음을 만족시키는 A를 구하기
$ x_1=\begin{bmatrix} 1 \ 0 \end{bmatrix}, \quad Ax_1=\begin{bmatrix} 2 \ 3 \ 4 \end{bmatrix} \qquad x_2=\begin{bmatrix} 0 \ 1 \end{bmatrix}, \quad Ax_2=\begin{bmatrix} 4 \ 6 \ 8 \end{bmatrix} $
$ A = \begin{bmatrix} 2 & 4 \ 3 & 6 \ 4 & 8 \end{bmatrix} \quad (A = A\cdot I = A\begin{bmatrix} x_1 x_2 \end{bmatrix} = \begin{bmatrix} Ax_1 Ax_2 \end{bmatrix}) $
Elementary basis 외의 다른 basis로 A를 만들 경우:
$ x_1=\begin{bmatrix} 1 \ 1 \end{bmatrix}, \quad Ax_1=\begin{bmatrix} 6 \ 9 \ 12 \end{bmatrix} \qquad x_2=\begin{bmatrix} 2 \ -1 \end{bmatrix}, \quad Ax_2=\begin{bmatrix} 0 \ 0 \ 0 \end{bmatrix} \quad \rightarrow \quad A = \begin{bmatrix} 6 & 0 \ 9 & 0 \ 12 & 0 \end{bmatrix} \quad $
$A\begin{bmatrix} -1 \ 2 \end{bmatrix} = \begin{bmatrix} 6 & 0 \ 9 & 0 \ 12 & 0 \end{bmatrix} \begin{bmatrix} -1 \ 2 \end{bmatrix} = \begin{bmatrix} -6 \ -9 \ -12 \end{bmatrix} $
$A\begin{bmatrix} -1 \ 2 \end{bmatrix} = A(x_1-x_2) = Ax_1 - Ax_2 = \begin{bmatrix} 6 \ 9 \ 12 \end{bmatrix} $
성립하지 않음.
Polynomial case: differentiation & Integration
- Elementary basis vector를 찾은 뒤
- Basis에 대해 transformation (matrix)를 결정해야한다.
예를 들어, degree 3 polynomial $P_3$, $\quad p(t)=a_0+a_1t+a_2t^2+a_3t^3$에 대해서
Basis for $P_3:\quad p_1=1, \quad p_2=t, \quad p_3=t^2, \quad p_4=t^3$
Differentiation: $A=d/dt$
각 polynomial basis를 vector form으로 나타내면,
$p_1=(1,0,0,0), \quad p_2=(0,1,0,0), \quad p_3=(0,0,1,0), \quad p_4=(0,0,0,1)$
$Ap_1=0. \quad Ap_2=1=p_1, \quad Ap_3=2t=2p_2, \quad Ap_4=3t^2=3p_3$
$ Ap_1 = \begin{bmatrix} 0 \ 0 \ 0 \ 0 \end{bmatrix}, \quad Ap_2 = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}, \quad Ap_3 = \begin{bmatrix} 0 \ 2 \ 0 \ 0 \end{bmatrix}, \quad Ap_1 = \begin{bmatrix} 0 \ 0 \ 3 \ 0 \end{bmatrix} $
$$ A_{diff} = \begin{bmatrix} 0 & 1 & 0 & 0 \ 0 & 0 & 2 & 0 \ 0 & 0 & 0 & 3 \ 0 & 0 & 0 & 0 \end{bmatrix} \qquad A\begin{bmatrix} a_0 \ a_1 \ a_2 \ a_3 \end{bmatrix} = \begin{bmatrix} a_1 \ 2a_2 \ 3a_3 \ 0 \end{bmatrix}, $$
Example: $p(t)=2+t+t^2+t^3$
$$ {dp \over dt} = Ap \rightarrow \begin{bmatrix} 0 & 1 & 0 & 0 \ 0 & 0 & 2 & 0 \ 0 & 0 & 0 & 3 \ 0 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} 2 \ 1 \ -1 \ -1 \end{bmatrix} = \begin{bmatrix} 1 \ -2 \ -3 \ 0 \end{bmatrix} \rightarrow 1-2t-3t^2 $$
Integration
Basis $\quad$ {$x_1=1, x_2=t, x_3=t^2, x_4=t^3$} $\quad \rightarrow \quad$ {$y_1=1, y_2=t, y_3=t^2, =t^3, y_5=t^4$}
$ \int_{0}^{t} 1, dt = t \quad or \quad Ax_1=y_2 \qquad \cdots \qquad \int_{0}^{t} t^4, dt = {1 \over 4}t^5 \quad or \quad Ax_4={1 \over 4}y_5 $
$$ A_{int} = \begin{bmatrix} 0 & 0 & 0 & 0 \ 1 & 0 & 0 & 0 \ 0 & {1 \over 2} & 0 & 0 \ 0 & 0 & {1 \over 3} & 0 \ 0 & 0 & 0 & {1 \over 4} \end{bmatrix} $$
Integration 뒤에 다시 differentiation을 하면 operation을 거치기 전의 원래 function으로 돌아간다. (Invertible)
$$ A_{diff}A_{int} = \begin{bmatrix} 1 & & & \ & 1 & & \ & & 1 & \ & & & 1 \end{bmatrix} $$
- Differentiation이 integration의 left-inverse.
- 순서를 바꾸면 성립하지 않는다. $A_{int}A_{diff}$ is not $I$
Rotations Q, Projections P, and Reflections H
Rotation
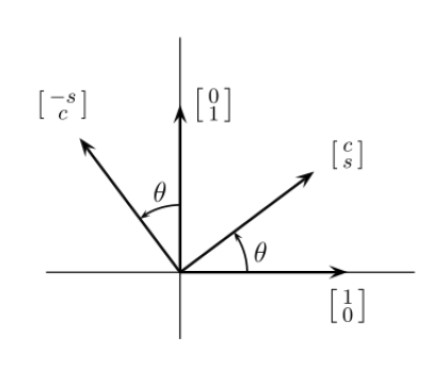
$ Q_\theta = \begin{bmatrix} 1 \ 0 \end{bmatrix} = \begin{bmatrix} cos\theta \ sin\theta \end{bmatrix}, \quad Q_\theta = \begin{bmatrix} 0 \ 1 \end{bmatrix} = \begin{bmatrix} -sin\theta \ cos\theta \end{bmatrix} $
$ Q_\theta = \begin{bmatrix} cos\theta & -sin\theta \ sin\theta & cos\theta \end{bmatrix} $
$Q_\theta^{-1} = Q_{-\theta} \qquad Q_\theta^2 = Q_{2\theta} \qquad Q_\theta Q_\phi = Q_{\theta+\phi}$
Projection

$ P_\theta = \begin{bmatrix} 1 \ 0 \end{bmatrix} = \begin{bmatrix} cos^2\theta \ sin\theta cos\theta \end{bmatrix}, \quad P_\theta = \begin{bmatrix} 0 \ 1 \end{bmatrix} = \begin{bmatrix} sin\theta cos\theta \ sin^2\theta \end{bmatrix} $
$ P_\theta = \begin{bmatrix} c^2 & cs \ cs & s^2 \end{bmatrix} $, Projection onto $\theta$-line
$P^2_\theta = P_\theta$, 한 번 projection한 이후로는 여러번 projection해도 제자리에 머무른다.
Reflection
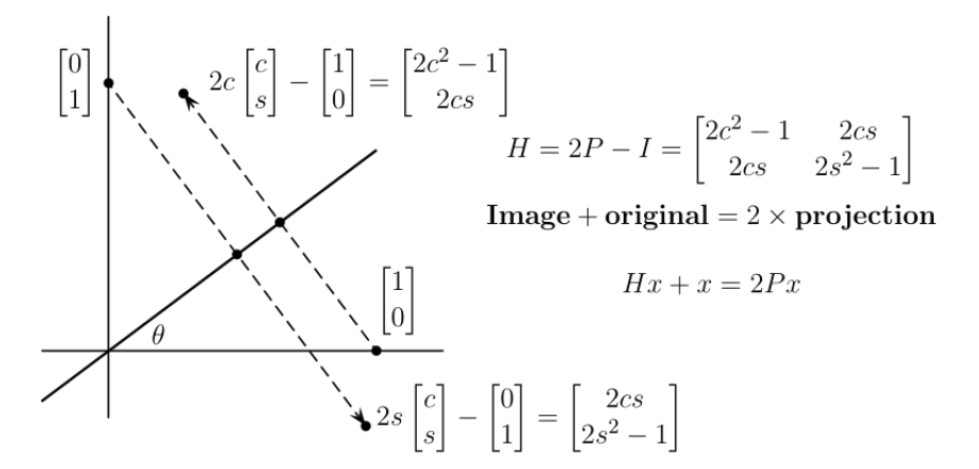
$ H_\theta = \begin{bmatrix} 2c^2-1 & 2cs \ 2cs & 2s^2-1 \end{bmatrix} = \begin{bmatrix} cos2\theta & sin2\theta \ sin2\theta & -cos2\theta \end{bmatrix} $
-
draft