Chapter 19. 탐욕 알고리즘의 이해
- TOC {:toc}
이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ‘Chapter 19. 탐욕 알고리즘의 이해’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.
강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 4. 탐욕 알고리즘의 이해에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.
내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
1. 탐욕 알고리즘이란?
- Greedy algorithm 또는 탐욕 알고리즘이라고 불림
- 최적의 해에 가까운 값을 구하기 위해 사용됨
- 완전히 최적의 해라고 보기는 어렵다.
- 여러 경우 중 하나를 결정해야 할 때마다, 매 순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행해서, 최종적인 값을 구하는 방식
2. 탐욕 알고리즘 예
문제 1: 동전 문제
지불해야 하는 값이 4720원 일 때 1원 50원 100원, 500원 동전으로 동전의 수가 가장 적게 지불하시오.
- 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식으로 구현 가능
- 탐욕 알고리즘으로 매 순간 최적이라고 생각되는 경우를 선택하면 됨
- 지금 순간에 가장 큰 값을 갖는 동전만 고려하기 때문에 탐욕 알고리즘으로 볼 수 있다.
# 리스트를 내림차순으로 정렬
coin_list = [1, 100, 50, 500]
print(coin_list)
# [1, 100, 50, 500]
coin_list.sort(reverse=True)
print(coin_list)
# [500, 100, 50, 1]
coin_list = [500, 100, 50, 1]
def min_coin_count(value, coin_list):
# 동전의 개수
total_coin_count = 0
# 어떤 동전이 몇 개 사용됐는지를 나타낸 함수
details = list()
# 동전을 내림차순으로 정렬
# 큰 값의 동전부터 사용하기 위함
coin_list.sort(reverse=True)
for coin in coin_list:
# 코인을 값으로 나눈 몫이 동전의 개수가 된다.
coin_num = value // coin
total_coin_count += coin_num
value -= coin_num * coin
details.append([coin, coin_num])
return total_coin_count, details
min_coin_count(4720, coin_list)
# (31, [[500, 9], [100, 2], [50, 0], [1, 20]])
문제2: 부분 배낭 문제 (Fractional Knapsack Problem)
무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣는 문제
- 각 물건은 무게(w)와 가치(v)로 표현될 수 있음
- 물건은 쪼갤 수 있기 때문에 물건 일부분이 배낭에 넣어질 수 있음, 그래서 Fractional Knapsack Problem으로 부름
- Fractional Knapsack Problem의 반대로 물건을 쪼개서 넣을 수 없는 배낭 문제도 존재함 (0/1 Knapsack Problem으로 부름)
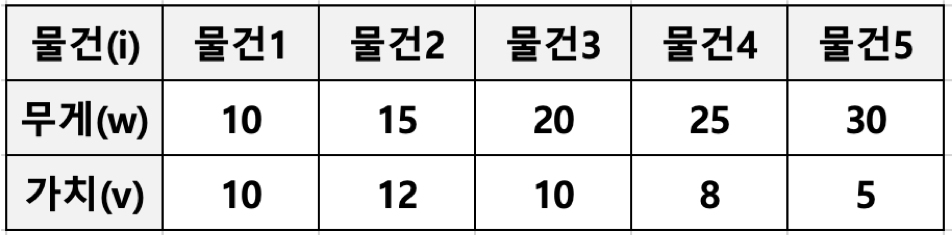
- 현재 상황에서 최적의 선택은 무게 대비 가치가 높은 것.
- 물건 1과 5를 비교했을 때, 물건 1을 넣는 것이 이득이다.
data_list = [(10, 10), (15, 12), (20, 10), (25, 8), (30, 5)]
# capacity: 무게 제한
def get_max_value(data_list, capacity):
# 무게(x[0]) 대비 가격(x[1])을 기준으로 내림차순으로 정렬한다.
data_list = sorted(data_list, key=lambda x: x[1] / x[0], reverse=True)
# 배낭 안의 전체 가치
total_value = 0
details = list()
for data in data_list:
# 현재 원소의 무게가 제한 이내이면
# 물건을 통째로 넣는다.
if capacity - data[0] >= 0:
# 제한에서 해당 물건의 무게를 빼준다.
capacity -= data[0]
# 전체 값에는 해당 물건의 가치를 더해준다.
total_value += data[1]
# fraction을 1로 해당 물건을 details에 추가한다.
details.append([data[0], data[1], 1])
else:
# 물건이 얼마나(fraction) 들어갈 수 있는지 구한다.
fraction = capacity / data[0]
# 위의 비율만큼 가치를 더해준다.
total_value += data[1] * fraction
# fraction을 위의 비율로 해당 물건을 details에 추가한다.
details.append([data[0], data[1], fraction])
# 더는 물건을 넣을 수 없기 때문에 break
break
return total_value, details
get_max_value(data_list, 30)
# (24.5, [[10, 10, 1], [15, 12, 1], [20, 10, 0.25]])
# 무게가 10, 15인 물건은 온전히 들어갔고
# 무게가 20인 물건은 1/4만 들어갔다.
3. 탐욕 알고리즘의 한계
- 탐욕 알고리즘은 근사치 추정에 활용
- 반드시 최적의 해를 구할 수 있는 것은 아니기 때문
- 최적의 해에 가까운 값을 구하는 방법의 하나임
예시
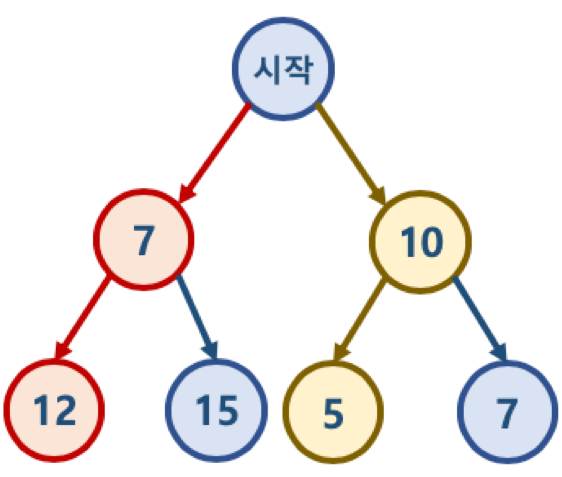
‘시작’ 노드에서 시작해서 가장 작은 값을 찾아 leaf node 까지 가는 경로를 찾을 시에
- Greedy 알고리즘 적용 시 ‘시작 -> 7 -> 12’를 선택하게 되므로 7 + 12 = 19가 됨
- 하지만 실제 가장 작은 값은 ‘시작 -> 10 -> 5’ 이며, 10 + 5 = 15가 답