Chapter 18. 그래프 기본 탐색 알고리즘: 깊이 우선 탐색(DFS)
- TOC {:toc}
이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 18. 그래프 기본 탐색 알고리즘: 너비 우선 탐색(BFS)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.
강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 2. 깊이 우선 탐색 (Depth-First Search)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.
내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
1. BFS 와 DFS 란?
- 그래프 탐색: 특정 노드를 찾아가는 것이다.
- 대표적인 그래프 탐색 알고리즘
- 너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 탐색하는 방식
- 깊이 우선 탐색 (Depth First Search): 정점의 자식들을 먼저 탐색하는 방식
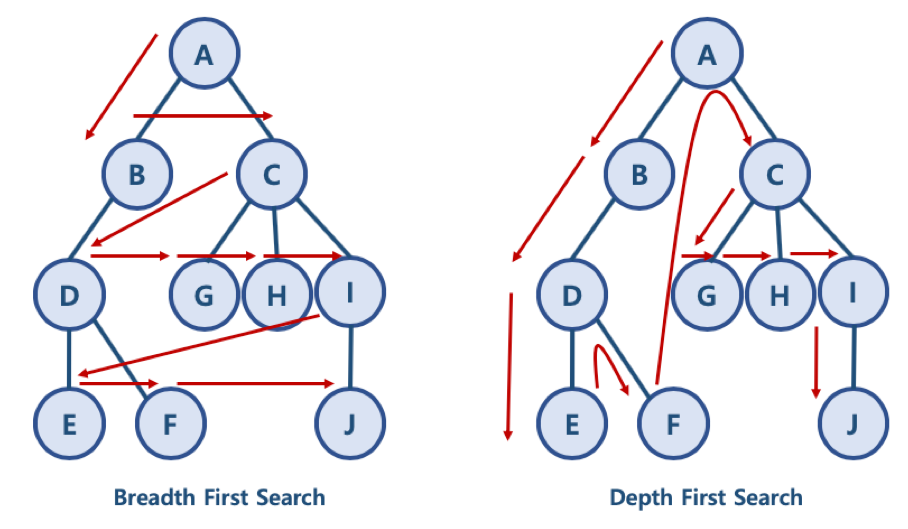
BFS/DFS 방식 이해를 위한 예제
- BFS 방식: A - B - C - D - G - H - I - E - F - J
- 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
- DFS 방식: A - B - D - E - F - C - G - H - I - J
- 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함
2. 파이썬으로 그래프를 표현하는 방법
- 파이썬에서 제공하는 딕셔너리와 리스트 자료 구조를 활용해서 그래프를 표현할 수 있음
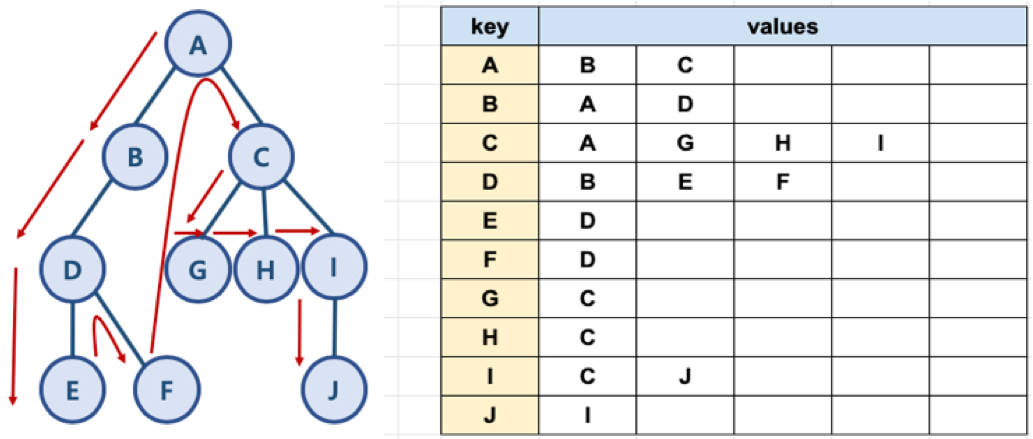
그래프 예와 파이썬 표현
- 노드는 딕셔너리의 key로 만든다.
- 해당 노드의 인접 노드들의 리스트를 value로 만든다.
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
graph
# 출력 결과
# {'A': ['B', 'C'],
# 'B': ['A', 'D'],
# 'C': ['A', 'G', 'H', 'I'],
# 'D': ['B', 'E', 'F'],
# 'E': ['D'],
# 'F': ['D'],
# 'G': ['C'],
# 'H': ['C'],
# 'I': ['C', 'J'],
# 'J': ['I']}
여기까지 BFS 강의 정리글과 내용이 동일하다.
3. DFS 알고리즘 구현
자료구조 스택과 큐를 활용함
need_visit스택과visited큐, 두 개의 자료 구조를 생성- BFS 자료구조는 두 개의 큐를 활용하는 데 반해, DFS는 스택과 큐를 활용한다는 차이가 있음을 인지해야 함
큐와 스택 구현은 별도 라이브러리를 활용할 수도 있지만, 간단히 파이썬 리스트를 활용할 수도 있음
- 딕셔너리에서 첫 key 값(e.g., A)을 꺼내
need_visit스택에 넣는다. need_visit스택에서 마지막 값을 pop 해visited큐에 존재하는지 확인한다.- 존재하지 않으면
visited큐에 넣는다.- 존재하면 아무것도 하지 않고
need_visit스택의 다음 값으로 넘어간다.
- 존재하면 아무것도 하지 않고
visited큐에 넣을 때마다 그 값을 key로 갖는 value(e.g., B, C)를need_visit스택에 넣는다.- 그래프에서 같은 depth를 갖는 노드의 순서는 따로 정해져 있지 않기 때문에 value 리스트의 값을
need_visit에 넣는 순서는 크게 상관없다.
- 그래프에서 같은 depth를 갖는 노드의 순서는 따로 정해져 있지 않기 때문에 value 리스트의 값을
- 위의 과정을 반복한다.
위 그림의 초반 진행 순서를 나타내면 다음과 같다.
| 순서 | 대기 | 큐 / 스택 | ||||||
|---|---|---|---|---|---|---|---|---|
| 0 | visited | |||||||
| need_visit | A | |||||||
| 1 | A | visited | ||||||
| need_visit | ||||||||
| 2 | visited | A | ||||||
| need_visit | B | C | ||||||
| 3 | C | visited | A | |||||
| need_visit | B | |||||||
| 4 | visited | A | C | |||||
| need_visit | B | A | G | H | I | |||
| 5 | I | visited | A | B | ||||
| need_visit | B | A | G | H | ||||
| 6 | visited | A | B | I | ||||
| need_visit | B | A | G | H | C | J | ||
| 7 | J | visited | A | C | I | |||
| need_visit | B | A | G | H | C | |||
| 8 | visited | A | B | I | J | |||
| need_visit | B | A | G | H | C | I | ||
| 9 | I | visited | A | C | I | J | ||
| need_visit | B | A | G | H | C | |||
| 10 | C | visited | A | C | I | J | ||
| need_visit | B | A | G | H | ||||
| … | … | … |
def dfs(graph, start_node):
visited, need_visit = list(), list()
need_visit.append(start_node)
# need_visit에 원소가 존재하는 동안
while need_visit:
# need_visit의 마지막 원소를 pop 한다.
node = need_visit.pop()
# node가 visited에 존재하지 않으면
if node not in visited:
# visited에 추가한 뒤
visited.append(node)
# 해당 값을 key로 갖는 value 리스트를 need_visit에 추가한다.
need_visit.extend(graph[node])
# 완성한 visited를 반환한다.
return visited
# 테스트 코드
dfs(graph, 'A') # ['A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E']
4. 시간 복잡도
일반적인 DFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 위 코드에서 while need_visit 은 V + E 번 만큼 수행함
- 시간 복잡도: O(V + E)