Chapter 15. 고급 정렬 알고리즘: 퀵 정렬(Quick Sort)
- TOC {:toc}
이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 15. 고급 정렬 알고리즘: 퀵 정렬(Quick Sort)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.
강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 9. 대표적인 정렬5: 퀵 정렬 (quick sort)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.
내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
1. 퀵 정렬 (quick sort) 이란?
- 정렬 알고리즘의 꽃
- ’기준점(pivot이라고 부름)’을 정해서, 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right)으로 모으는 함수를 작성함
- 각 왼쪽(left), 오른쪽(right)은 ‘재귀 용법’을 사용해서 다시 동일 함수를 호출하여 위 작업을 반복함
- 함수는 왼쪽(left) + 기준점(pivot) + 오른쪽(right)을 반환함
퀵 정렬 과정
pivot을 선택한다. 보통 처음으로는 첫 값을 선택한다.
| pivot | p | |||||||
|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 숫자 | 49 | 97 | 53 | 5 | 33 | 65 | 62 | 51 |
각 값을 비교하면서 pivot 기준으로 그보다 작은 값은 왼쪽, 큰 값은 오른쪽에 놓는다.
| pivot | p | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 3 | 4 | 0 | 1 | 2 | 5 | 6 | 7 | ||
| 숫자 | 5 | 33 | 49 | 97 | 53 | 65 | 62 | 51 |
pivot으로 나눈 각 부분에 위의 작업을 반복한다.
-
왼쪽
pivot p 인덱스 3 4 숫자 5 33 pivot p 인덱스 3 4 숫자 5 33 -
오른쪽
pivot p 인덱스 1 2 5 6 7 숫자 97 53 65 62 51 pivot p 인덱스 2 5 6 7 1 숫자 53 65 62 51 97
왼쪽은 정렬이 끝났으므로 종결하고 오른쪽은 다시 작업을 반복한다.
-
오른쪽 - 왼쪽
pivot p 인덱스 2 5 6 7 숫자 53 65 62 51 pivot p 인덱스 7 2 5 6 숫자 51 53 65 62 -
오른쪽 - 왼쪽 - 오른쪽
pivot p 인덱스 5 6 숫자 65 62 pivot p 인덱스 6 5 숫자 62 65
나눠서 정렬한 부분들을 합쳐나간다.
-
오른쪽 - 왼쪽 - 오른쪽
pivot p 인덱스 6 5 숫자 62 65 -
오른쪽 - 왼쪽
pivot p 인덱스 7 2 6 5 숫자 51 53 62 65 -
오른쪽
pivot p 인덱스 7 2 6 5 1 숫자 51 53 62 65 97 -
왼쪽
pivot p 인덱스 3 4 숫자 5 33 -
전체
pivot p 인덱스 3 4 0 7 2 6 5 1 숫자 5 33 49 51 53 62 65 97 pivot 인덱스 3 4 0 7 2 6 5 1 숫자 5 33 49 51 53 62 65 97
2. 어떻게 코드로 만들까?
퀵소트 알고리즘에 대해서는 위에서 언급이 되었으므로, 이를 구현하기 위한 세부 코드에 대해 연습을 통해 이해합니다.
프로그래밍 연습 1
다음 리스트를 리스트 슬라이싱(예 [:2])을 이용해서 세 개로 잘라서 각 리스트 변수에 넣고 출력해보기
data_list = [1, 2, 3, 4, 5]
data1 = data_list[:2]
data2 = data_list[2]
data3 = data_list[3:]
# 테스트 코드
print (data1) # [1, 2]
print (data2) # 3
print (data3) # [4, 5]
프로그래밍 연습 2
다음 리스트를 맨 앞에 데이터를 pivot 변수에 넣고, pivot 변숫값을 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
data_list = [4, 1, 2, 5, 7]
인덱스 순회
for index in range(1, 5):
print (index)
# 출력 결과
# 1
# 2
# 3
# 4
data_list = [4, 1, 2, 5, 7]
left = list()
right = list()
pivot = data_list[0]
for index in range(1, 5):
if data_list[index] < pivot:
left.append(data_list[index])
else:
right.append(data_list[index])
# 테스트 코드
print (left) # [1, 2]
print (right) # [5, 7]
프로그래밍 연습 3
data_list 가 임의 길이일 때 리스트를 맨 앞에 데이터를 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣기
import random
data_list = random.sample(range(100), 10)
left = list()
right = list()
pivot = data_list[0]
for index in range(1, -----------------):
if data_list[index] < pivot:
left.append(data_list[index])
else:
right.append(data_list[index])
import random
data_list = random.sample(range(100), 10)
left = list()
right = list()
pivot = data_list[0]
for index in range(1, len(data_list)):
if data_list[index] < pivot:
left.append(data_list[index])
else:
right.append(data_list[index])
# 테스트 코드
print (left, pivot, right) # [37, 27, 52, 10, 2] 65 [85, 66, 78, 74]
프로그래밍 연습 4
data_list 가 다음 세 데이터를 가지고 있을 때 리스트를 맨 앞에 데이터를 기준으로 작은 데이터는 left 변수에, 그렇지 않은 데이터는 right 변수에 넣고 left, right, pivot 변숫값을 사용해서 정렬된 데이터 출력해보기
data_list = [4, 3, 2]
left = list()
right = list()
pivot = data_list[0]
for index in range(1, len(data_list)):
if data_list[index] < pivot:
left.append(data_list[index])
else:
right.append(data_list[index])
# 테스트 코드
print (left, pivot, right) # [3, 2] 4 []
3. 알고리즘 구현
quicksort 함수 만들기
- 만약 리스트 개수가 한 개면 해당 리스트 반환
- 그렇지 않으면, 리스트 맨 앞의 데이터를 기준점(pivot)으로 놓기
- left, right 리스트 변수를 만들고,
- 맨 앞의 데이터를 뺀 나머지 데이터를 기준점과 비교(pivot)
- 기준점보다 작으면 left.append(해당 데이터)
- 기준점보다 크면 right.append(해당 데이터)
- return quicksort(left) + pivot + quicksort(right) 로 재귀 호출
- 리스트로 만들어서 반환하기: return quick_sort(left) + [pivot] + quick_sort(right)
def qsort(list):
# 데이터가 1개일 때 해당 데이터만 들어 있는 리스트를 반환
# 재귀 용법 종결조건
if len(list) <= 1:
return list
left, right = list(), list()
# 첫 값을 pivot으로 설정한다.
pivot = list[0]
for n in range(1, len(list)):
# pivot보다 작으면
if pivot > list[n]:
# left에 추가
left.append(list[n])
else:
# right에 추가
right.append(list[n])
# left, pivot, right을 합친 리스트를 반환한다.
return qsort(left) + [pivot] + qsort(right)
# 테스트 코드
import random
data_list = random.sample(range(100), 10)
qsort(data_list) # [2, 20, 35, 39, 49, 51, 57, 74, 82, 94]
프로그래밍 연습 5
위 퀵 정렬 코드를 파이썬 list comprehension을 사용해서 더 깔끔하게 작성해보기
def qsort(data):
if len(data) <= 1:
return data
pivot = data[0]
left = [ item for item in data[1:] if pivot > item ]
right = [ item for item in data[1:] if pivot <= item ]
return qsort(left) + [pivot] + qsort(right)
# 테스트 코드
import random
data_list = random.sample(range(100), 10)
qsort(data_list) # [5, 10, 37, 43, 61, 71, 77, 78, 82, 84]
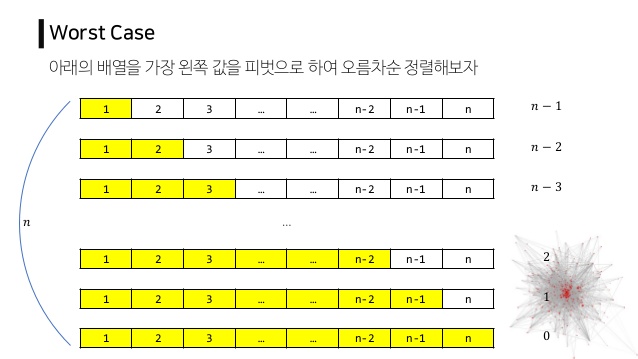
4. 알고리즘 분석
- 병합 정렬과 유사, 시간복잡도는 $O(n\log n)$
- 단, 최악의 경우
- 맨 처음 pivot이 가장 크거나, 가장 작으면
- 모든 데이터를 비교하는 상황이 나옴: $O(n^2)
- 단, 최악의 경우