Chapter 15. 고급 정렬 알고리즘: 병합 정렬(Merge Sort)
- TOC {:toc}
이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 15. 고급 정렬 알고리즘: 병합 정렬(Merge Sort)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.
강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 8. 대표적인 정렬4: 병합 정렬 (merge sort)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.
내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
1. 병합 정렬 (merge sort)
- 재귀 용법을 활용한 정렬 알고리즘
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting
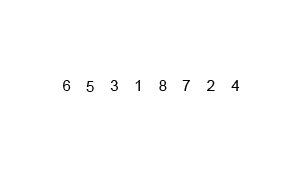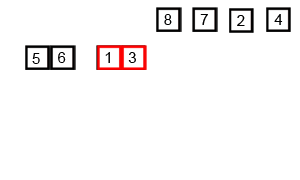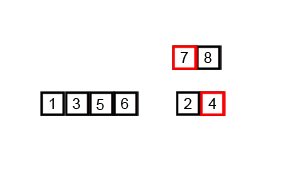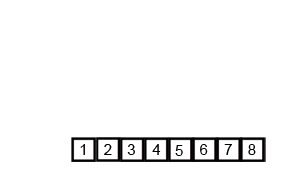
출처: https://ko.wikipedia.org/wiki/합병_정렬
2. 알고리즘 이해
예시 데이터가 네 개일 때
데이터 개수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해보자.
예: data_list = [1, 9, 3, 2]
- 먼저 [1, 9], [3, 2] 로 나누고
- 다시 앞부분은 [1], [9] 로 나누고
- 다시 정렬해서 합친다. [1, 9]
- 다음 [3, 2] 는 [3], [2] 로 나누고
- 다시 정렬해서 합친다 [2, 3]
- 이제 [1, 9] 와 [2, 3]을 합친다.
- 1 < 2 이니 [1]
- 9 > 2 이니 [1, 2]
- 9 > 3 이니 [1, 2, 3]
- 9 밖에 없으니, [1, 2, 3, 9]
병합 정렬 과정
분리(split) 단계
| 단계 | 0 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 숫자 | 49 | 97 | 53 | 5 | 33 | 65 | 62 | 51 |
| 단계 | 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 숫자 | 49 | 97 | 53 | 5 | 33 | 65 | 62 | 51 |
| 단계 | 2 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||||
| 숫자 | 49 | 97 | 53 | 5 | 33 | 65 | 62 | 51 |
병합(merge) 단계
| 단계 | 0 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |||
| 숫자 | 49 | 97 | 5 | 53 | 33 | 65 | 51 | 62 |
- 왼쪽과 오른쪽의 인덱스 번호를 순회하면서 비교해서 정렬한다.
- 왼쪽의 0번 값(49)과 오른쪽의 0번 값(5)을 비교한다. 5를 가장 앞에 둔다.
- 왼쪽의 0번 값(49)과 오른쪽의 1번 값(53)을 비교한다. 49를 다음에 둔다.
- 왼쪽의 1번 값(97)과 오른쪽의 1번 값(53)을 비교한다. 53을 다음에 둔다.
- 남은 왼쪽의 1번 값(97)을 마지막에 둔다.
| 단계 | 1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | |
| 숫자 | 5 | 49 | 53 | 97 | 33 | 51 | 62 | 65 |
| 단계 | 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 숫자 | 5 | 33 | 49 | 51 | 53 | 62 | 65 | 97 |
3. 알고리즘 구현
리스트를 나누는 함수와 합치는 함수가 필요하다.
- 데이터가 1개가 남을 때까지 나눈다.
- 나누는 함수는 재귀 용법으로 짧게 구현할 수 있다.
- 나눈 데이터들을 정렬하면서 합친다.
mergesplit 함수 만들기
- 만약 리스트 개수가 한 개면 해당 값 반환
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
left = mergesplit(앞)right = mergesplit(뒤)merge(left, right)
merge 함수 만들기
- 리스트 변수 하나 만들기 (sorted)
left_index, right_index = 0while left_index < len(left) or right_index < len(right):- 만약 left_index 나 right_index 가 이미 left 또는 right 리스트를 다 순회했다면, 그 반대쪽 데이터를 그대로 넣고, 해당 인덱스 1 증가
if left[left_index] < right[right_index]:sorted.append(left[left_index])left_index += 1
else:1sorted.append(right[right_index])right_index += 1
작은 부분부터 작성해서 하나씩 구현하기
프로그래밍 연습 1
어떤 데이터리스트가 있을 때 리스트를 앞뒤로 자르는 코드 작성해보기 (일반화)
def split_func(data):
medium = int(len(data) / 2)
print (medium)
left = data[:medium]
right = data[medium:]
print (left, right)
split_func([1, 5, 3, 2, 4])
# 2
# [1, 5] [3, 2, 4]
재귀 용법 활용하기
프로그래밍 연습 2
다음 문장을 코드로 작성해보기 (merge 함수는 아직은 없는 상태, 있다고만 가정)
mergesplit 함수 만들기
- 만약 리스트 개수가 한 개면 해당 값 반환
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
- left = mergesplit(앞)
- right = mergesplit(뒤)
- merge(left, right)
def mergesplit(data):
if len(data) <= 1:
return data
medium = int(len(data) / 2)
left = mergesplit(data[:medium])
right = mergesplit(data[medium:])
return merge(left, right)
merge 함수 만들기
- 목표: left와 right의 리스트 데이터를 정렬해서 sorted_list 라는 이름으로 return 하기
- left와 right는 이미 정렬된 상태 또는 데이터가 하나임
프로그래밍 연습 3
- left부터 하나씩 right과 비교
- left > right이면, left를 sorted_list에 넣고, 다음 left 리스트와 right 비교
- 그렇지않으면 반대로 하기
다음 경우만 프로그래밍으로 작성해보기
left = [0]
right = [3]
결과는 별도의 리스트 변수를 만들어 적은 숫자 순으로 순서대로 저장해서 리턴
프로그래밍 연습 4
다음 경우만 프로그래밍으로 작성해보기
left = [0, 2]
right = [1]
결과는 별도의 리스트 변수를 만들어 적은 숫자 순으로 순서대로 저장해서 리턴
프로그래밍 연습 5
다음 경우만 프로그래밍으로 작성해보기
left = [0, 2]
right = [1, 3]
결과는 별도의 리스트 변수를 만들어 적은 숫자 순으로 순서대로 저장해서 리턴
프로그래밍 연습 6
left, right 리스트 변수의 데이터 수가 한 개에서 여러 개가 될 수 있을 때 작성해보기(일반화)
- sorted_list 리스트 변수 선언하기
- left_index, right_index를 0으로 초기화하기
- while left_index < len(left) or right_index < len(right) 이면,
- 만약 left_index >= len(left)이면, sorted_list에 right[right_index]를 추가하고, right_index 값을 1 증가
- 만약 right_index >= len(right)이면, sorted_list에 left[left_index]를 추가하고, left_index 값을 1 증가
- 만약 left[left_index] < right[right_index]이면, sorted_list 에 left[left_index] 를 추가하고, left_index 값을 1증가
- 위 세 가지가 아니면, sorted_list 에 right[right_index] 를 추가하고, right_index 값을 1증가
최종 코드
def merge(left, right):
# 새로운 리스트를 생성한다.
merged = list()
left_point, right_point = 0, 0
# case1 - left/right 둘 다 있을 때
# left point가 left 안에 있고 right point도 right 안에 존재하는 동안
while len(left) > left_point and len(right) > right_point:
# left point의 값이 right point의 값보다 크면
if left[left_point] > right[right_point]:
# merged에 right를 추가하고
merged.append(right[right_point])
# right point를 다음으로 이동한다.
right_point += 1
else:
# merged에 left를 추가하고
merged.append(left[left_point])
# left point를 다음으로 이동한다.
left_point += 1
# case2 - left 데이터만 남아있을 때
while len(left) > left_point:
merged.append(left[left_point])
left_point += 1
# case3 - right 데이터만 남아있을 때
while len(right) > right_point:
merged.append(right[right_point])
right_point += 1
return merged
병합 정렬 최종 코드
merge + mergesplit
def merge(left, right):
merged = list()
left_point, right_point = 0, 0
while len(left) > left_point and len(right) > right_point:
if left[left_point] > right[right_point]:
merged.append(right[right_point])
right_point += 1
else:
merged.append(left[left_point])
left_point += 1
while len(left) > left_point:
merged.append(left[left_point])
left_point += 1
while len(right) > right_point:
merged.append(right[right_point])
right_point += 1
return merged
def mergesplit(data):
if len(data) <= 1:
return data
medium = int(len(data) / 2)
left = mergesplit(data[:medium])
right = mergesplit(data[medium:])
return merge(left, right)
# 테스트 코드
import random
data_list = random.sample(range(100), 10)
mergesplit(data_list)
# [8, 12, 24, 40, 47, 70, 81, 87, 92, 96]
4. 알고리즘 분석
알고리즘 분석은 쉽지 않음, 이 부분은 참고로만 알아두자
다음을 보고 이해해보자
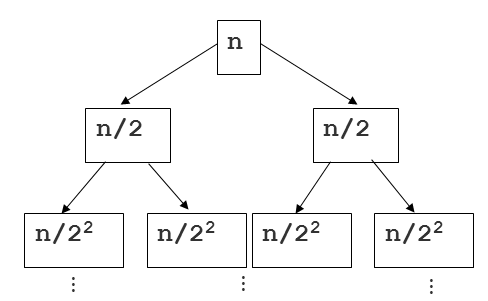
- 몇 단계 깊이까지 만들어지는지를 depth라고 하고 i로 놓자. 맨 위 단계는 0으로 놓자.
- 다음 그림에서 ${n/2}^2$ 2 는 2단계 깊이라고 해보자
- 각 단계에 있는 하나의 노드 안의 리스트 길이는 ${n/2}^2$가 된다.
- 각 단계에는 $2^i$개의 노드가 있다.
- 따라서, 각 단계는 항상 $2i \times n/2^i=O(n)$
- 단계는 항상 $\log _2n$ 개 만큼 만들어짐,시간 복잡도는 결국 $O(\log n)$, 2는 역시 상수이므로 삭제
- 따라서, 단계별 시간 복잡도 $O(n) \times O(\log n) = O(n\log n)$