Chapter 14. 동적 계획법(Dynamic Programming)과 분할 정복(Divide and Conquer)

TOC {:toc}

이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 14. 동적 계획법(Dynamic Programming)과 분할 정복(Divide and Conquer)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.

강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 7. 동적 계획법 (Dynamic Programming)과 분할 정복 (Divide and Conquer)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.

내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.

1. 정의

동적 계획법 (DP 라고 많이 부름)

입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘
상향식 접근법으로, 가장 최하위 해답을 구한 후, 이를 저장하고, 해당 결괏값을 이용해서 상위 문제를 풀어가는 방식
Memoization 기법을 사용함
- Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술
문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨
- 예: 피보나치 수열

분할 정복

문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
하향식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀 함수로 구현
문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- 예: 병합 정렬, 퀵 정렬 등

2. 공통점과 차이점

공통점

문제를 잘게 쪼개서, 가장 작은 단위로 분할

차이점

동적 계획법
- 부분 문제는 중복되어, 상위 문제 해결 시 재활용됨
- Memoization 기법 사용 (부분 문제의 해답을 저장해서 재활용하는 최적화 기법으로 사용)
분할 정복
- 부분 문제는 서로 중복되지 않음
- Memoization 기법 사용 안 함

3. 동적 계획법 알고리즘 이해

프로그래밍 연습

피보나치 수열: n을 입력받아서 다음과 같이 계산됨

$$ F_n := \begin{cases} 0 & \text{if} \quad n = 0\ 1 & \text{if} \quad n = 1\ F_{n-1} + F_{n-2} & \text{if} \quad n > 1 \end{cases} $$

# 함수를 fibonacci 라고 하면,

fibonacci(0) # 0
fibonacci(1) # 1
fibonacci(2) # 1
fibonacci(3) # 2
fibonacci(4) # 3
fibonacci(5) # 5
fibonacci(6) # 8
fibonacci(7) # 13
fibonacci(8) # 21
fibonacci(9) # 34

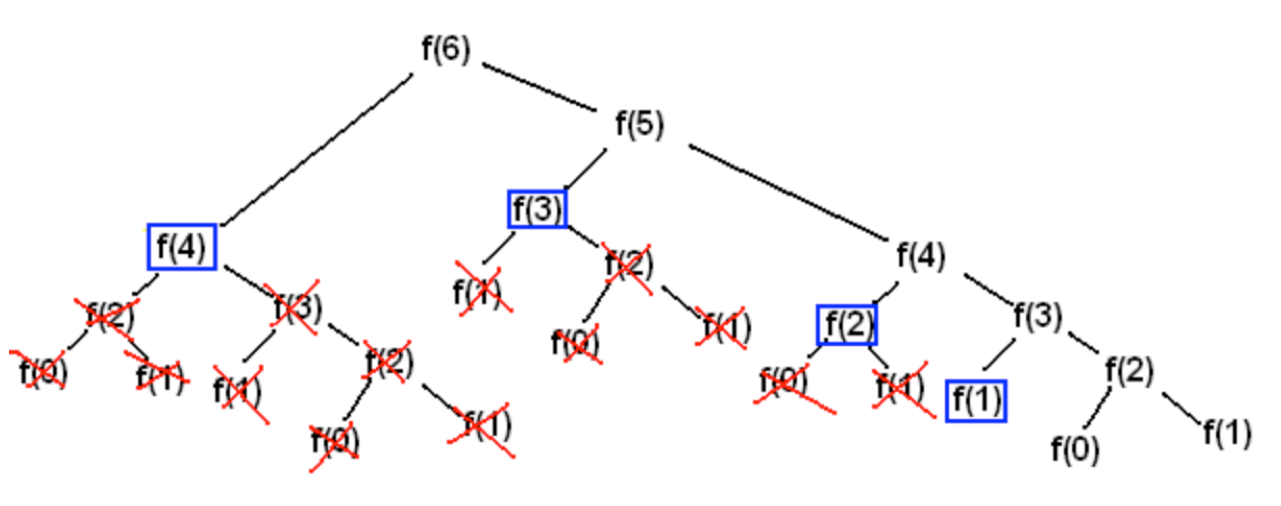
fibonacci

f(n)을 f(0), f(1)과 같은 작은 단위로 쪼개야 하고
그 과정에서 f(0), f(1) 등은 중복해서 여러 번 구한다는 점에서
동적 계획법의 예시라고 할 수 있다.

n을 입력받았을 때 피보나치 수열로 결괏값을 출력하세요

재귀 호출을 활용

def fibo(num):
    # num이 0이나 1이면
    if num <= 1:
        return num
    return fibo(num - 1) + fibo(num - 2)

# 테스트 코드
fibo(4) # 3

동적 계획법 활용

def fibo_dp(num):
    # 저장 공간을 생성한다.
    # 0 ~ num 까지의 인덱스에 각각 0을 저장
    cache = [ 0 for index in range(num + 1)]
      
    # 초깃값을 입력한다.
    cache[0] = 0
    cache[1] = 1

    # 나머지 값도 계산해서 대입한다.
    for index in range(2, num + 1):
        # 매번 1까지 계산하는 것이 아니라 이미 계산해 저장된 값을 바로 이용한다.
        cache[index] = cache[index - 1] + cache[index - 2]
    return cache[num]

# 테스트 코드
fibo(10) # 55

실행 코드를 보며 이해해보기: 코드 분석

분할 정복 알고리즘의 예는 별도 챕터에서 다루는 병합 정렬과 퀵 정렬을 통해 이해