Chapter 13. 재귀 용법(Recursive Call)

TOC {:toc}

이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 13. 재귀 용법(Recursive Call)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.

강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 6. 재귀 용법 (recursive call, 재귀 호출)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.

내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.

재귀 용법 (recursive call, 재귀 호출)

고급 정렬 알고리즘에서 재귀 용법을 사용하므로, 고급 정렬 알고리즘을 익히기 전에 재귀 용법을 먼저 익히기로 합니다.

1. 재귀 용법 (recursive call, 재귀 호출)

함수 안에서 동일한 함수를 호출하는 형태
여러 알고리즘 작성 시 사용되므로, 익숙해져야 함

2. 재귀 용법 이해

예제를 풀어보며, 재귀 용법을 이해해보기

예제: 팩토리얼을 구하는 알고리즘을 Recursive Call을 활용해서 알고리즘 작성하기

분석하기

간단한 경우부터 생각해보기
- 2! = 1 X 2
- 3! = 1 X 2 X 3
- 4! = 1 X 2 X 3 X 4 = 4 X 3!
규칙이 보임: n! = n X (n - 1)!
1. 함수를 하나 만든다.
2. 함수(n) 은 n > 1 이면 return n X 함수(n - 1)
3. 함수(n) 은 n = 1 이면 return n
검증 (코드로 검증하지 않고, 직접 간단한 경우부터 대입해서 검증해야 함)
1. 먼저 2! 부터
  - 함수(2) 이면, 2 > 1 이므로 2 X 함수(1)
  - 함수(1) 은 1 이므로, return 2 X 1 = 2 맞다!
2. 먼저 3! 부터
  - 함수(3) 이면, 3 > 1 이므로 3 X 함수(2)
  - 함수(2) 는 결국 1번에 의해 2! 이므로, return 2 X 1 = 2
  - 3 X 함수(2) = 3 X 2 = 3 X 2 X 1 = 6 맞다!
3. 먼저 4! 부터
  - 함수(4) 이면, 4 > 1 이므로 4 X 함수(3)
  - 함수(3) 은 결국 2번에 의해 3 X 2 X 1 = 6
  - 4 X 함수(3) = 4 X 6 = 24 맞다!

코드 레벨로 적어보기

def factorial(num):
    if num > 1:
        return num * factorial(num - 1)
    # num이 1보다 작은 경우 (0, 1인 경우만 생각한다)
    else:
        # 1을 그대로 반환한다.
        return num
 
# 테스트 코드
for num in range(10):
    print (factorial(num))

# 출력 결과
# 0
# 1
# 2
# 6
# 24
# 120
# 720
# 5040
# 40320
# 362880

예제 - 시간 복잡도와 공간 복잡도

factorial(n) 은 n - 1 번의 factorial() 함수를 호출해서, 곱셈을 함
- 일종의 n - 1 번 반복문을 호출한 것과 동일
- factorial() 함수를 호출할 때마다, 지역변수 n이 생성됨
시간 복잡도/공간 복잡도는 O(n-1) 이므로 결국, 둘 다 O(n)

3. 재귀 호출의 일반적인 형태

일반적인 형태 1

def function(입력):
    # 입력이 일정 값 이상이면
    if 입력 > 일정값:
        # 입력보다 작은 값
        return function(입력 - 1)
    else:
        # 재귀 호출 종료
        return 일정값, 입력값, 또는 특정값 

일반적인 형태 2

def function(입력):
    # 입력이 일정 값보다 작으면
    if 입력 <= 일정값: 
        # 재귀 호출 종료
        return 일정값, 입력값, 또는 특정 값
    function(입력보다 작은 값)
    return 결괏값

위의 예시를 두 번째 형태로 나타내보면 다음과 같다.

def factorial(num):
    if num <= 1:
        return num

    return num * factorial(num - 1)
 
# 테스트 코드
for num in range(10):
    print (factorial(num))

# 출력 결과
# 0
# 1
# 2
# 6
# 24
# 120
# 720
# 5040
# 40320
# 362880

재귀 호출은 스택의 전형적인 예

함수는 내부적으로 스택처럼 관리된다.

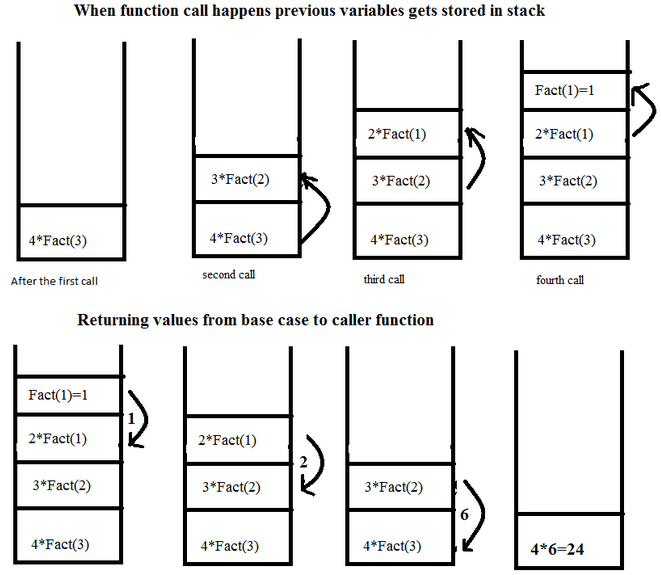
recursive call

재귀 호출이 이해가 가지 않는다면? - 코드 분석

참고: 파이썬에서 재귀 함수는 깊이가(한 번에 호출되는 함수의 개수) 1000회 이하가 되어야 함.

스택 공간이 1000회를 호출할 만큼으로 제한되어 있다고 볼 수 있다.

4. 재귀 용법을 활용한 프로그래밍 연습

프로그래밍 연습 1

다음 함수를 재귀 함수를 활용해서 완성해서 1부터 num까지의 곱이 출력되게 만드세요

코드 개요

def muliple(data):
    if data <= 1:
        return data

    # 재귀를 작성할 부분
    return -------------------------

# 테스트 코드
multiple(10)

작성 코드: 반복문 사용

def multiple(num):
    return_value = 1
    for index in range(1, num + 1):
        return_value = return_value * index
    return return_value

작성 코드: 재귀 용법 사용

def multiple(num):
    if num <= 1:
        return num
    return num * multiple(num - 1)
 
# 테스트 코드
multiple(10) # 3628800

프로그래밍 연습 2

숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 반환 함수를 만드세요. (재귀 함수를 써보세요)

참고: 임의 값으로 리스트 만들기

import random
# random.sample(범위, 개수)
# 범위: e.g., 0 ~ 99까지 중에서
# 개수: e.g., 임의로 10개를 만들어서 10개 값을 가지는 리스트 변수 만들기
data = random.sample(range(100), 10)
data
 
# 출력 결과
[72, 50, 8, 38, 77, 32, 90, 48, 74, 79]

코드 개요

def sum_list(data):
    if len(data) == 1:
        return data[0]

    # 재귀를 작성하는 부분
    return --------------------------------

# 테스트 코드
import random
data = random.sample(range(100), 10)
print (sum_list(data))

작성 코드

def sum_list(data):
    if len(data) <= 1:
        return data[0]
    # 0번 데이터와 1번 ~ 마지막까지 리스트의 sum_list를 호출한 값의
    # 합을 반환한다.
    return data[0] + sum_list(data[1:])

# 테스트 코드
sum_list(data) # 568

프로그래밍 연습 3

회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함 회문을 판별할 수 있는 함수를 재귀 함수를 활용해서 만들어봅니다.

참고 - 리스트 슬라이싱

string = 'Dave'
# 문자의 마지막
string[-1] # e
string[0] # D
# 1부터 -1(마지막)'전'까지
string[1:-1] # av
# 처음부터 마지막 전까지
string[:-1] # Dav

def palindrome(string):
    if len(strung) <= 1:
        return True

    if string[0] == string[-1]:
        # 현재 리스트의 두 번째부터 마지막 직전값까지(양 끝을 제외)를
        # 다시 함수로 넘긴다.
        return palindrome(string[1:-1])
    else:
        return False

프로그래밍 연습 4

정수 n에 대해
n이 홀수이면 3 X n + 1을 하고,
n이 짝수이면 n을 2로 나눕니다.
이렇게 계속 진행해서 n이 결국 1이 될 때까지 2와 3의 과정을 반복합니다.

예를 들어 n에 3을 넣었을 때 결과는 다음과 같습니다.

이렇게 정수 n을 입력받아, 위 알고리즘에 의해 1이 되는 과정을 모두 출력하는 함수를 작성하세요.

작성 코드

def func(n):
    print (n)
    # n이 1이면 n을 반환하고 종결
    if n == 1:
        return n

    if n % 2 == 1:
        return (func((3 * n) + 1))
    else:
        return (func(int(n / 2)))

# 테스트 코드
func(3)

# 출력 결과
# 3
# 10
# 5
# 16
# 8
# 4
# 2
# 1

프로그래밍 연습 5

정수 4를 1, 2, 3의 조합으로 나타내는 방법은 다음과 같이 총 7가지가 있다.

1+1+1+1
1+1+2
1+2+1
2+1+1
2+2
1+3
3+1

정수 n이 입력으로 주어졌을 때, n을 1, 2, 3의 합으로 나타낼 방법의 수를 구하시오

출처: ACM-ICPC > Regionals > Asia > Korea > Asia Regional - Taejon 2001

힌트

정수 n을 만들 수 있는 경우의 수를 반환하는 함수를 f(n) 이라고 하면,
f(n)은 f(n-1) + f(n-2) + f(n-3) 과 동일하다는 패턴 찾기

문제 분석을 연습장에 작성해 본 예

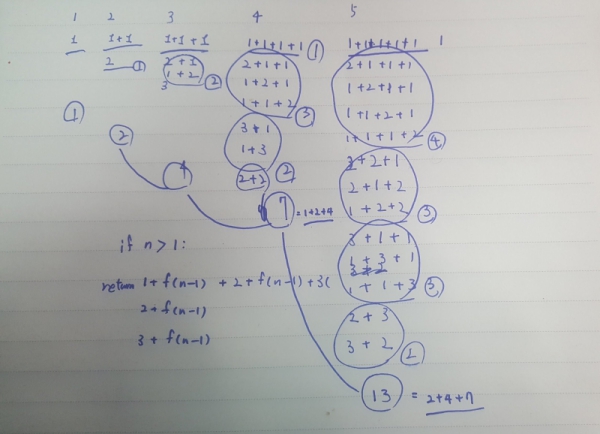
algorithm practice

작성 코드

def func(data):
    if data == 1:
        return 1
    elif data == 2:
        return 2
    elif data == 3:
        return 4

    return func(data - 1) + func(data - 2) + func(data - 3)

# 테스트 코드
func(5) # 13