Chapter 12. 기본 정렬 알고리즘: 버블 정렬(Bubble Sort)
- TOC {:toc}
이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 12. 정렬: 버블 정렬(Bubble Sort)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.
강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 3. 대표적인 정렬1: 버블 정렬 (bubble sort)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.
내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
0. 알고리즘 연습 방법
- 알고리즘을 잘 작성하기 위해서는 잘 작성된 알고리즘을 이해하고, 스스로 만들어봐야 함
- 모사! 그림을 잘 그리기 위해서는 잘 그린 그림을 모방하는 것부터 시작
- 모사를 하는 것처럼 기존에 잘 만들어진 알고리즘을 이해하는 것이 우선되어야 한다.
알고리즘 연습 방법 (모사 방법)
먼저 알고리즘은 연습장에 고안한 뒤 그다음에 코드로 옮겨야 한다.
- 연습장과 펜을 준비하자.
- 알고리즘 문제를 읽고 분석한 후에,
- 간단하게 테스트용으로 매우 간단한 경우부터 복잡한 경우 순서대로 생각해보면서, 연습장과 펜을 이용하여 알고리즘을 생각해본다.
- 가능한 알고리즘이 보인다면, 구현할 알고리즘을 세부 항목으로 나누고, 문장으로 세부 항목을 나누어서 적어본다.
- 코드화하기 위해, 데이터 구조 또는 사용할 변수를 정리하고,
- 각 문장을 코드 레벨로 적는다.
- 데이터 구조 또는 사용할 변수가 코드에 따라 어떻게 변하는지를 손으로 적으면서, 임의 데이터로 코드가 정상 동작하는지를 연습장과 펜으로 검증한다.
1. 정렬 (sorting) 이란?
- 정렬 (sorting): 어떤 데이터들이 주어졌을 때 이를 정해진 순서대로 나열하는 것
- 정렬은 프로그램 작성 시 빈번하게 필요로 함
- 다양한 알고리즘이 고안되었으며, 알고리즘 학습의 필수
다양한 정렬 알고리즘 이해를 통해, 동일한 문제에 대해 다양한 알고리즘이 고안될 수 있음을 이해하고, 각 알고리즘 간 성능 비교를 통해, 알고리즘 성능 분석에 대해서도 이해할 수 있음
2. 버블 정렬 (bubble sort) 이란?
- 두 인접한 데이터를 비교해서, 앞에 있는 데이터가 뒤에 있는 데이터보다 크면, 자리를 바꾸는 정렬 알고리즘
직접 눈으로 보면 더 이해가 쉽다: https://visualgo.net/en/sorting
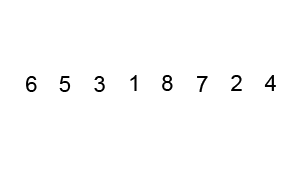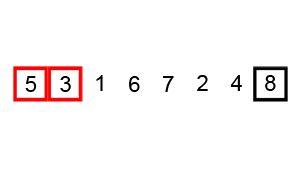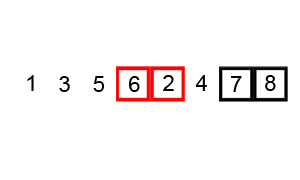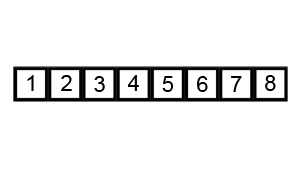
출처: https://en.wikipedia.org/wiki/Bubble_sort
3. 어떻게 코드로 만들까?
알고리즘 연습 방법에 기반해서 단계별로 생각해봅니다.
데이터가 두 개 있을 때
프로그래밍 연습: 데이터가 두 개일 때 버블 정렬 알고리즘 방식으로 정렬해보세요
| 단계 | 0 | 1 | |||
|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 0 | 1 | |
| 숫자 | 5 | 2 | 2 | 5 |
- 0번과 1번을 비교했을 때 5 < 2 이므로 자리를 바꾼다.
데이터가 세 개 있을 때
프로그래밍 연습: 데이터가 세 개일 때 버블 정렬 알고리즘 방식으로 정렬해보세요
| 단계 | 0 | 1 | 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | ||
| 숫자 | 5 | 4 | 2 | 4 | 5 | 2 | 4 | 2 | 5 |
- 0번과 1번을 비교했을 때 5 > 4 이므로 자리를 바꾼다.
- 1번과 2번을 비교했을 때 5 > 2 이므로 자리를 바꾼다.
| 단계 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 0 | 1 | 2 | |
| 숫자 | 2 | 4 | 5 | 2 | 4 | 5 |
- 다시 0번과 1번을 비교했을 때 4 > 2 이므로 자리를 바꾼다.
- 1번과 2번을 비교했을 때 4 < 5 이므로 자리를 바꾸지 않는다.
데이터가 네 개 있을 때
프로그래밍 연습: 데이터가 네 개일 때 버블 정렬 알고리즘 방식으로 정렬해보세요
| 단계 | 0 | 1 | 2 | 3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | |||
| 숫자 | 5 | 2 | 3 | 1 | 2 | 5 | 3 | 1 | 2 | 3 | 5 | 1 | 2 | 3 | 1 | 5 |
- 0번과 1번을 비교했을 때 5 > 2 이므로 자리를 바꾼다.
- 1번과 2번을 비교했을 때 5 > 3 이므로 자리를 바꾼다.
- 2번과 3번을 비교했을 때 5 > 1 이므로 자리를 바꾼다.
| 단계 | 4 | 5 | 6 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | ||
| 숫자 | 2 | 3 | 1 | 5 | 2 | 1 | 3 | 5 | 2 | 1 | 3 | 5 |
- 0번과 1번을 비교했을 때 2 < 3 이므로 자리를 바꾸지 않는다.
- 1번과 2번을 비교했을 때 3 > 1 이므로 자리를 바꾼다.
- 2번과 3번을 비교했을 때 3 < 5 이므로 자리를 바꾸지 않는다.
| 단계 | 7 | 8 | 9 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 인덱스 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | ||
| 숫자 | 1 | 2 | 3 | 5 | 1 | 2 | 3 | 5 | 1 | 2 | 3 | 5 |
- 0번과 1번을 비교했을 때 2 > 1 이므로 자리를 바꾼다.
- 1번과 2번을 비교했을 때 2 < 3 이므로 자리를 바꾸지 않는다.
- 2번과 3번을 비교했을 때 3 < 5 이므로 자리를 바꾸지 않는다.
4. 알고리즘 구현
특이점 찾아보기
- n개의 리스트가 있는 경우 최대 n - 1번의 로직을 적용한다.
- n - 1번의 턴을 돈다.
- 로직을 1번 적용할 때마다 가장 큰 숫자가 뒤에서부터 1개씩 결정된다.
- 한 번 턴을 돌면 현재 비교한 데이터 중 가장 큰 값이 가장 뒤로 가기 때문에 방금 정렬이 끝난 마지막 원소는 비교할 필요 없다.
- 로직이 때에 따라 일찍 끝날 수도 있다. 따라서 로직을 적용할 때 한 번도 데이터가 교환된 적이 없다면 이미 정렬된 상태이므로 로직을 더 반복 적용할 필요가 없다.
이를 반영한 코드 흐름
for num in range(len(data_list))반복swap = 0(교환이 되었는지를 확인하는 변수를 두자)- 반복문 안에서 n - 1번 반복해야 하므로,
for index in range(len(data_list) - num - 1) - 반복문 안의 반복문 안에서,
if data_list[index] > data_list[index + 1]이면 - swap:
data_list[index], data_list[index + 1] = data_list[index + 1], data_list[index] swap += 1- 반복문 안에서,
if swap == 0이면,break끝
def bubblesort(data):
# 데이터의 길이(n) - 1번 반복한다.
for index in range(len(data) - 1):
# swap 여부를 확인하는 swap을 False로 두고
swap = False
# 반복마다 이미 정렬된 원소 이전까지
for index2 in range(len(data) - index - 1):
# 현재 값이 다음 값보다 크면
if data[index2] > data[index2 + 1]:
# 두 값을 swap하고
data[index2], data[index2 + 1] = data[index2 + 1], data[index2]
# swap을 True로 바꾼다.
swap = True
# 반복하는 동안 swap이 한 번도 일어나지 않아
# swap이 여전히 False이면
if swap == False:
# 전체 반복을 종료한다.
break
# data를 반환한다.
return data
# 테스트 코드
# 랜덤 데이터를 얻기 위한 라이브러리
import random
data_list = random.sample(range(100), 50)
print (bubblesort(data_list))
5. 알고리즘 분석
- 반복문이 두 개: $O(n^2)$
- 최악의 경우, $n(n − 1) / 2$
- 최선(완전 정렬이 되어 있는 상태)의 경우 $O(n)$