Chapter 11. 힙(Heap)
- toc {:toc}
이 글은 패스트 캠퍼스 기술면접 완전 정복 올인원 패키지 Online ’Chapter 11. 힘(Heap)’의 강의내용을 정리하기 위해 강의 자료를 기반으로 작성한 글입니다.
강의 노트는 강의 구매자에게만 제공되는 자료이긴 하지만 잔재미 코딩의 10. 대표적인 자료구조: 힙 (Heap)에서 동일한 자료를 제공하고 있기 때문에 해당 자료를 기반으로 정리한 글을 작성해서 올립니다. 혹시 문제가 되는 경우 바로 내릴 예정이니 알려주시면 감사하겠습니다.
내용을 이해하기 위한 개인적인 설명이나 해석이 있을 수 있기 때문에 되도록 원문을 참고해주시길 바랍니다. 잘못된 부분이 있다면 댓글이나 그 외 편하신 방법으로 알려주시면 감사하겠습니다.
1. 힙(heap)이란?
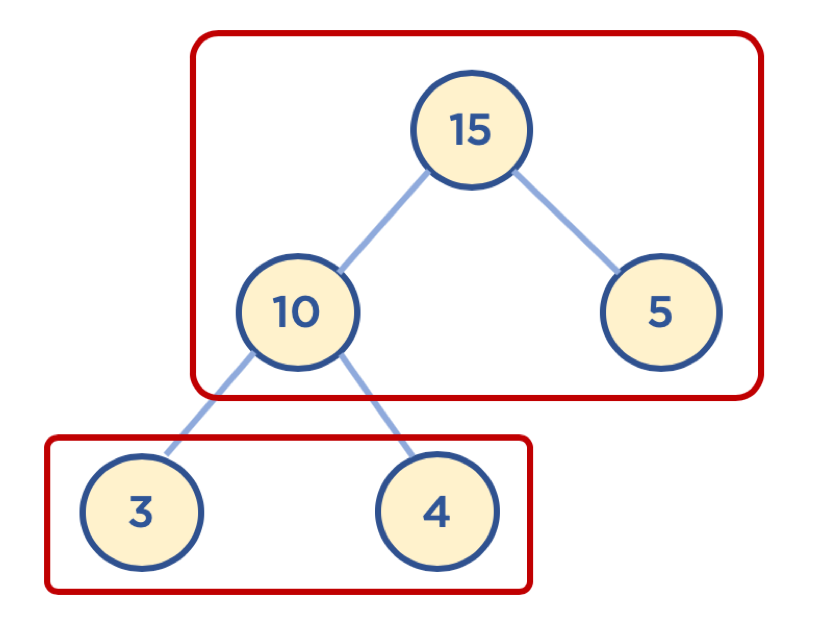
- 힙: 데이터에서 최댓값과 최솟값을 빠르게 찾기 위해 고안된 완전 이진 트리(complete binary tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
- 힙을 사용하는 이유
- 배열에 데이터를 넣고, 최댓값과 최솟값을 찾으려면 o(n) 이 걸림
- 이에 반해, 힙에 데이터를 넣고, 최댓값과 최솟값을 찾으면, $o(\log n)$ 이 걸림
- 우선순위 큐와 같이 최댓값 또는 최솟값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨
2. 힙(heap) 구조
- 힙은 최댓값을 구하기 위한 구조 (최대 힙, max heap) 와, 최솟값을 구하기 위한 구조 (최소 힙, min heap) 로 분류할 수 있음
- 힙은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
- 최소 힙의 경우는 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작음
- 완전 이진 트리 형태를 가짐
- 데이터를 채워 넣을 때 왼쪽 하단부터 채워 넣은 트리이다.
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
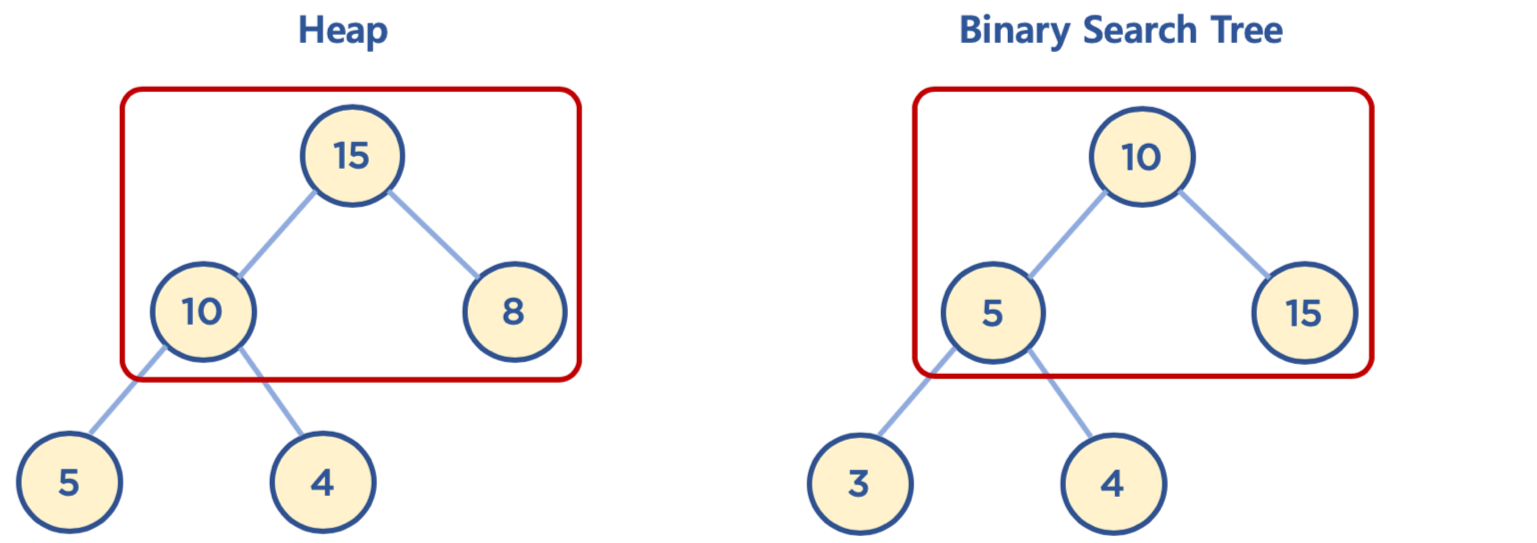
힙과 이진 탐색 트리의 공통점과 차이점
- 공통점
- 힙과 이진 탐색 트리는 모두 이진 트리임
- 차이점:
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음(max heap의 경우)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그다음 부모 노드, 그다음 오른쪽 자식 노드 값이 가장 큼
- 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 힙의 왼쪽 및 오른쪽 자식 노드의 값은 오른쪽이 클 수도 있고, 왼쪽이 클 수도 있음
- 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최솟값 검색을 위한 구조 중 하나로 이해하면 됨
3. 힙 (heap) 동작
- 데이터를 힙 구조에 삽입, 삭제하는 과정을 그림을 통해 선명하게 이해하기
힙에 데이터 삽입하기 - 기본 동작
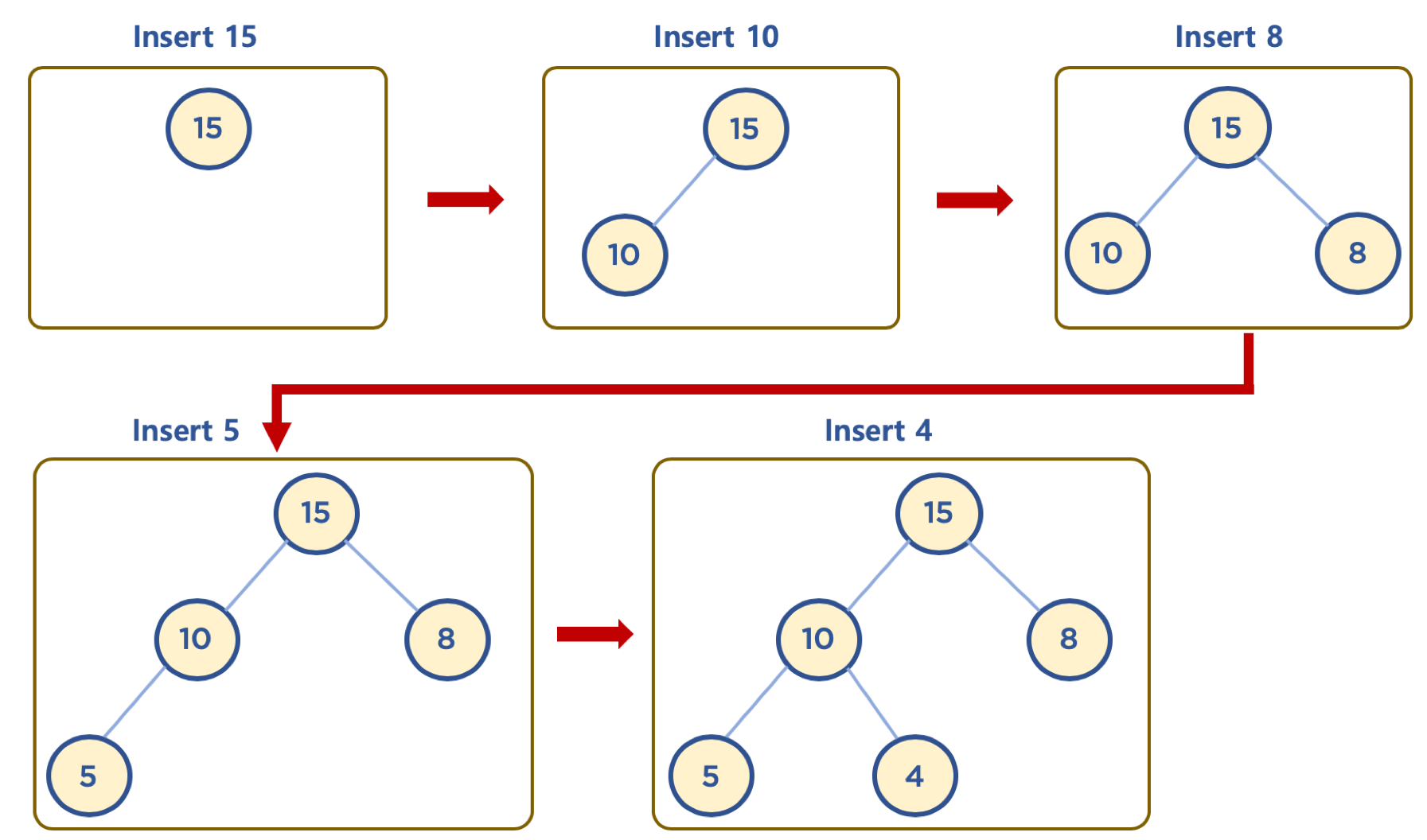
- 힙은 완전 이진 트리이므로, 삽입할 노드는 기본적으로 왼쪽 최하단부 노드부터 채워지는 형태로 삽입
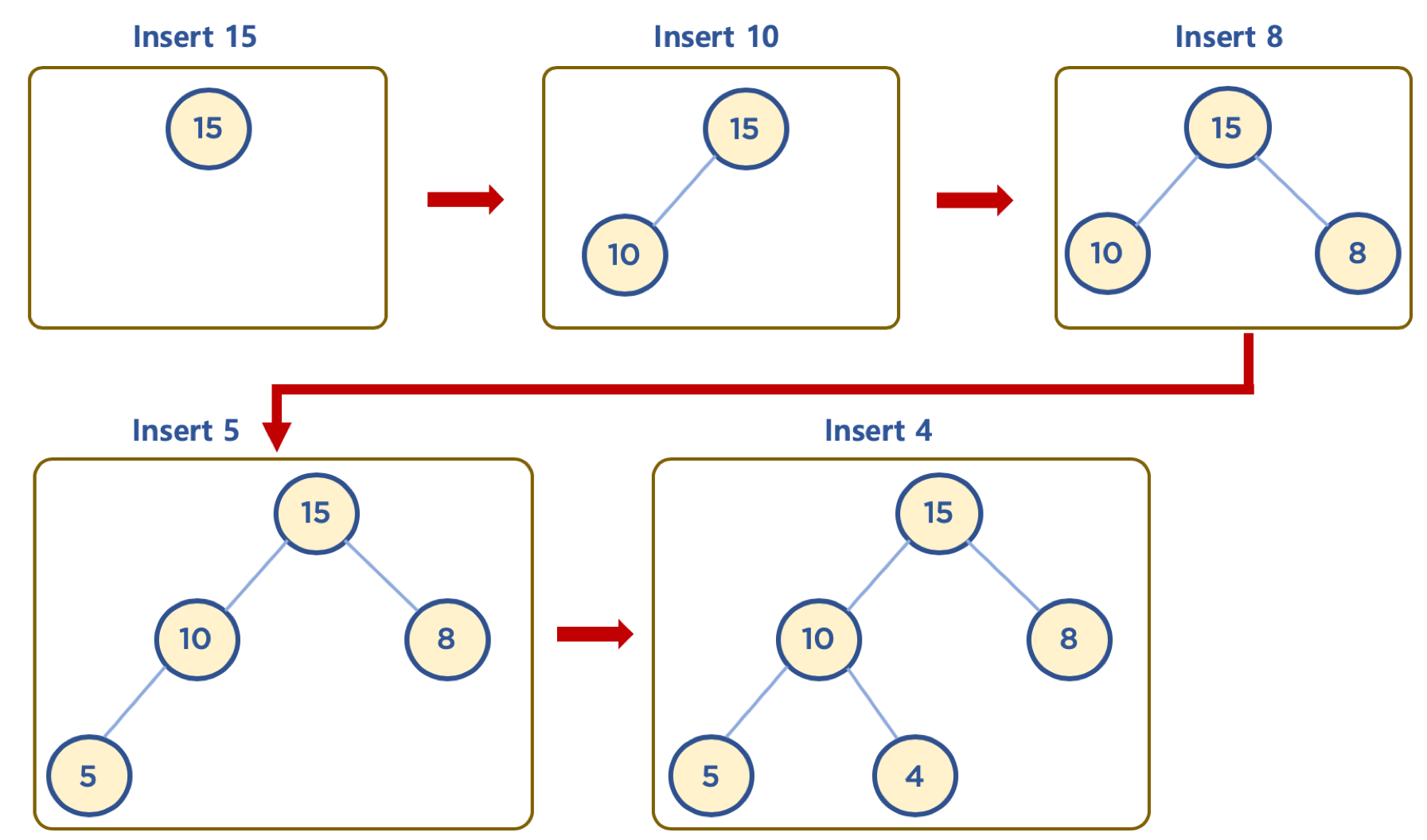
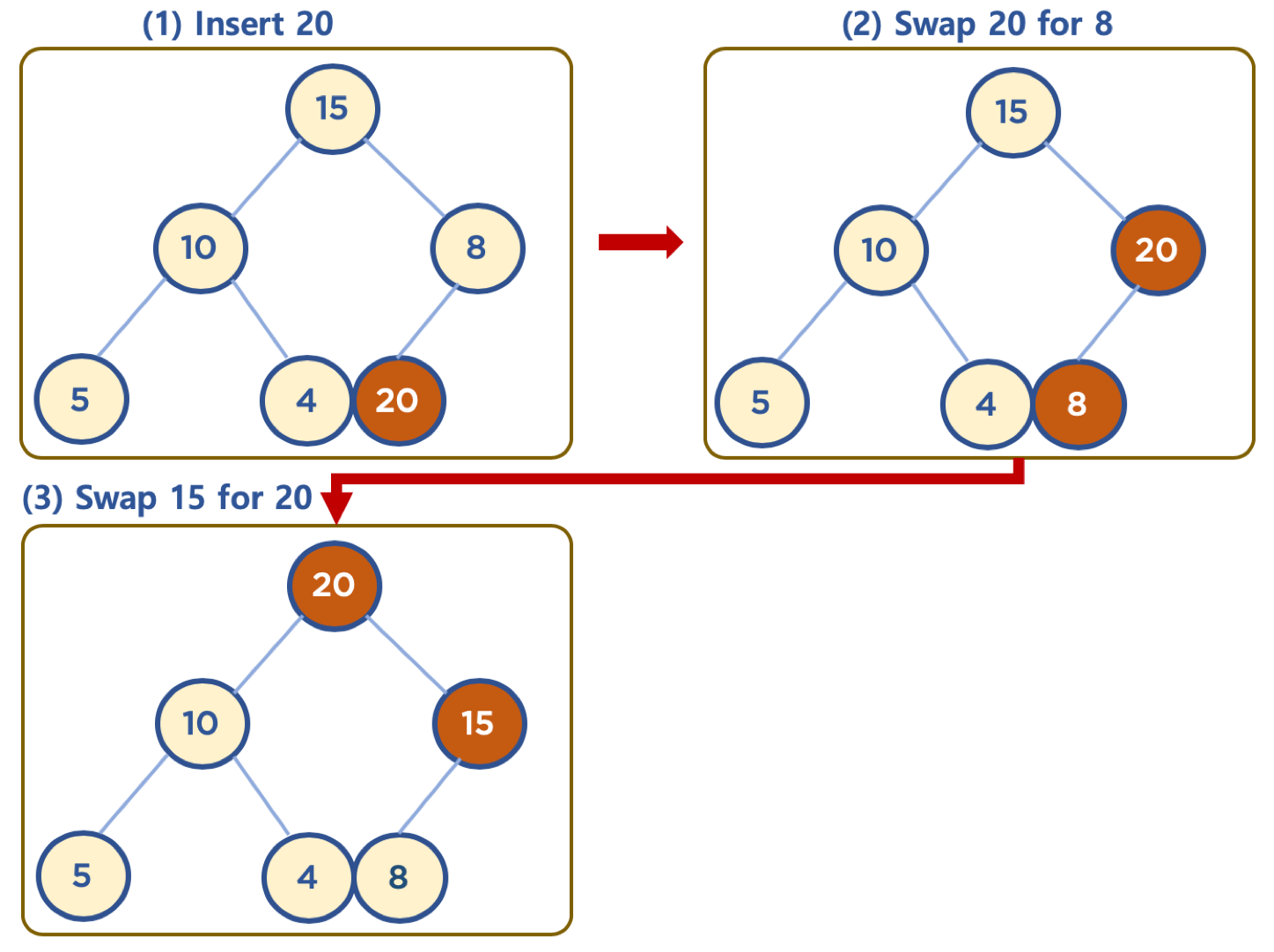
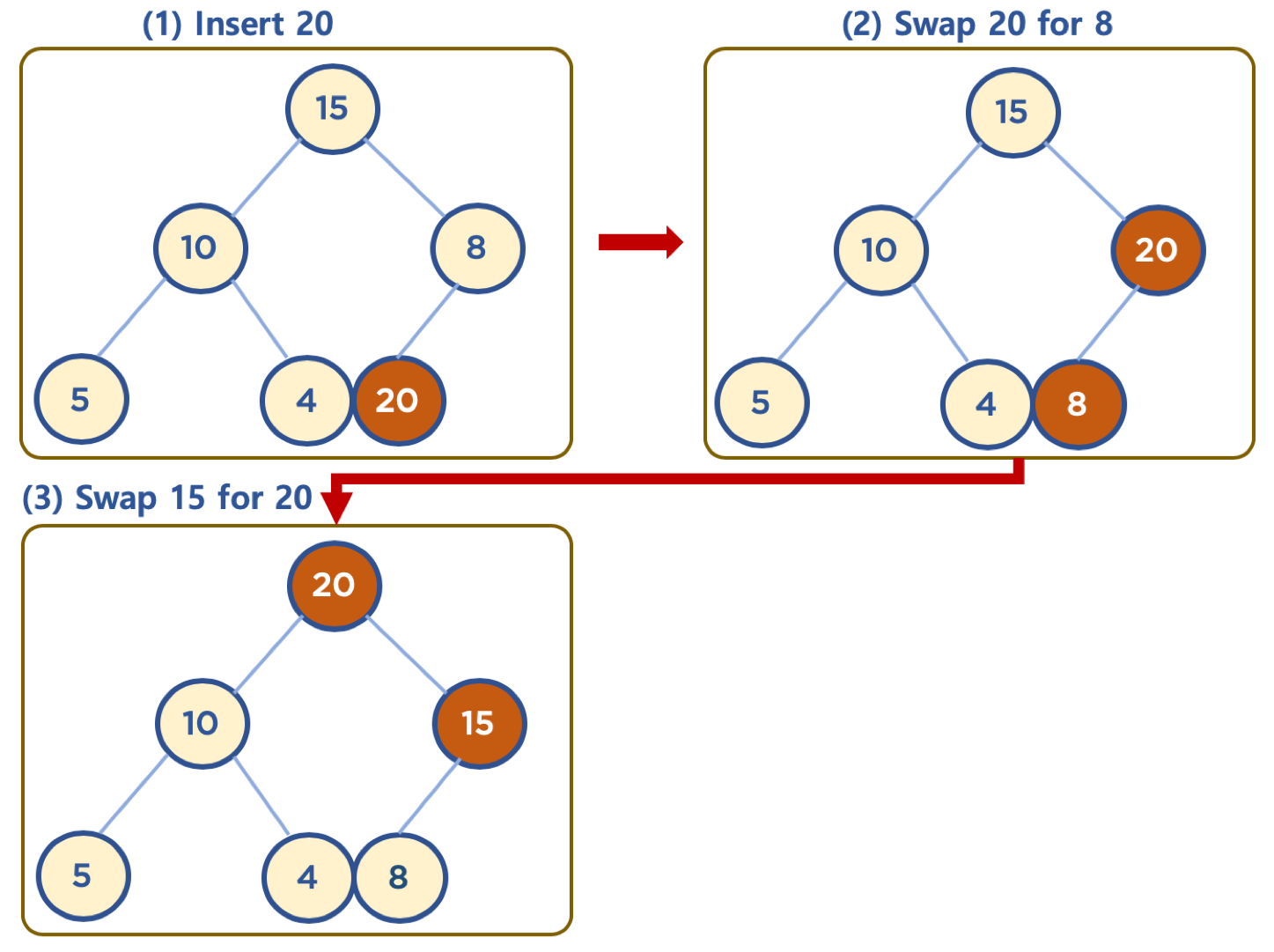
힙에 데이터 삽입하기 - 삽입할 데이터가 힙의 데이터보다 클 경우 (max heap의 예)
- 먼저 삽입된 데이터는 완전 이진 트리 구조에 맞추어, 최하단부 왼쪽 노드부터 채워짐
- 채워진 노드 위치에서, 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복함 (swap)
힙의 데이터 삭제하기 (max heap 의 예)
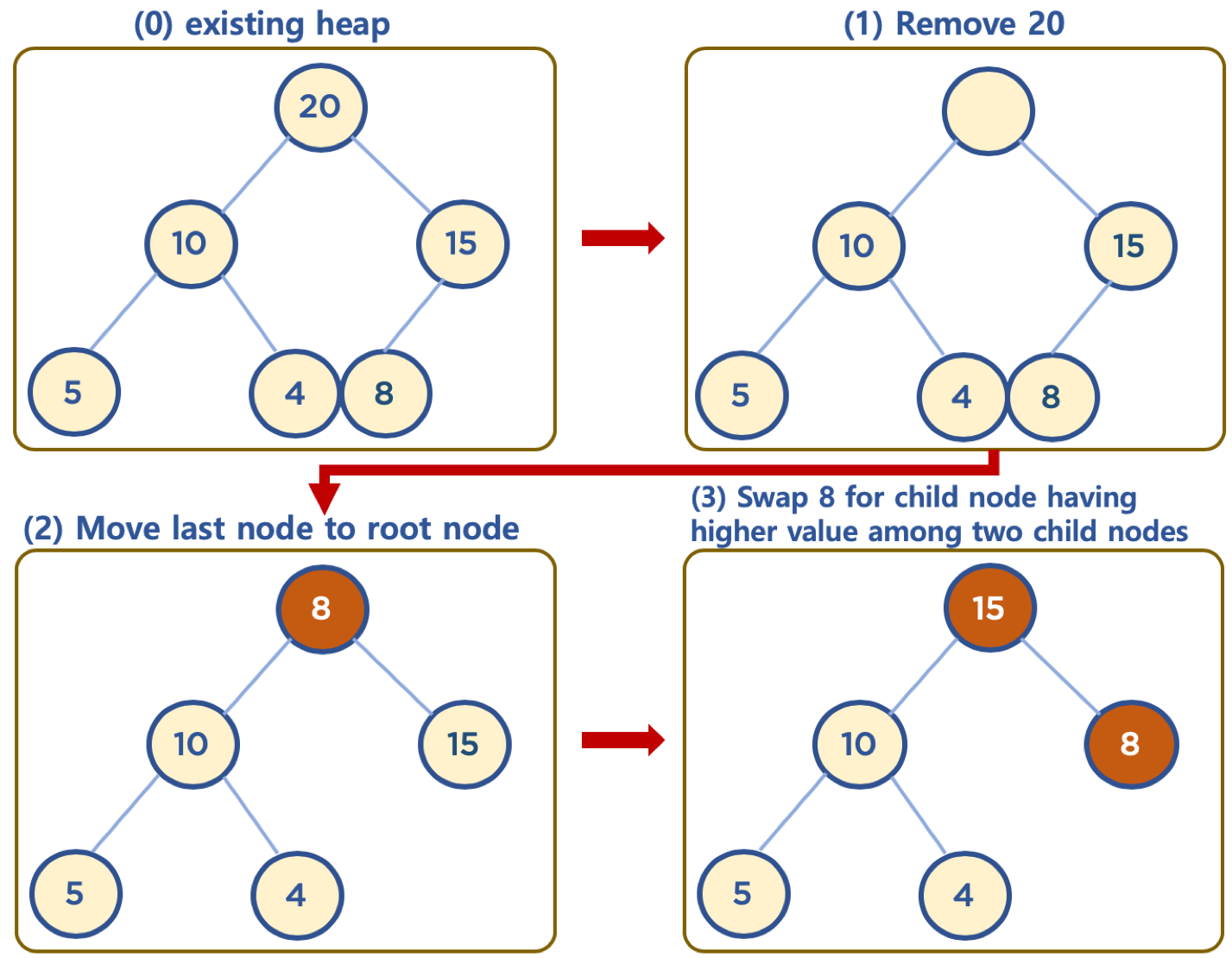
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최댓값 또는 최솟값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
- 상단의 데이터 삭제 시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드)를 root 노드로 이동
- root 노드의 값이 child node보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
4. 힙 구현
힙과 배열
- 일반적으로 힙 구현 시 배열 자료구조를 활용함
- 배열은 인덱스가 0번부터 시작하지만, 힙 구현의 편의를 위해, root 노드 인덱스 번호를 1로 지정하면, 구현이 좀 더 수월함
- 부모 노드 인덱스 번호 (parent node’s index) = 자식 노드 인덱스 번호 (child node’s index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2 + 1
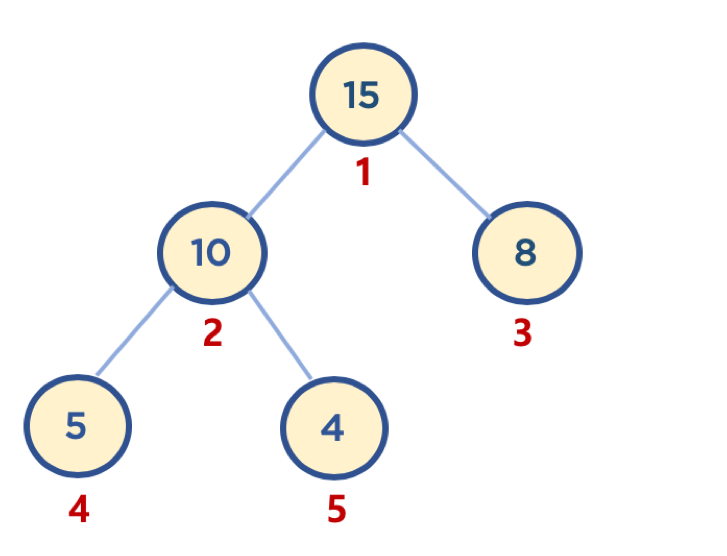
# 예1 - 10 노드의 부모 노드 인덱스
5 // 2 # 2, 5번 노드의 부모 노드는 2
2 // 2 # 1, 2번 노드의 부모 노드는 1
# 예1 - 15 노드의 왼쪽 자식 노드 인덱스 번호
2 * 2 # 4, 2번 노드의 왼쪽 자식은 4
1 * 2 # 2, 1번 노드의 왼쪽 자식은 2
# 예1 - 15 노드의 오른쪽 자식 노드 인덱스 번호
2 * 2 + 1 # 5, 2번 노드의 오른쪽 자식은 5
힙에 데이터 삽입 구현 (max heap 예)
- 힙 클래스 구현 1
class heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(none) # 0번 인덱스는 비워둔다.
self.heap_array.append(data)
heap = heap(1)
heap.heap_array # [none, 1]
- 힙 클래스 구현 2 - insert 1
- 우선 노드를 가장 마지막에 추가한다.
- 인덱스 번호는 1번부터 시작하도록 변경
class heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(none)
self.heap_array.append(data)
def insert(self, data):
if len(self.heap_array) == 0:
self.heap_array.append(none)
self.heap_array.append(data)
return true
# heap.array의 맨 끝에 data를 추가한다.
self.heap_array.append(data)
return true
- 힙 클래스 구현 3 - insert 2
- 삽입한 노드가 부모 노드의 값보다 클 경우, 부모 노드와 삽입한 노드 위치를 바꿈
- 삽입한 노드가 루트 노드가 되거나, 부모 노드보다 값이 작거나 같을 경우까지 반복
- 참고: 특정 노드의 관련 노드 위치 알아내기
- 부모 노드 인덱스 번호 (parent node’s index) = 자식 노드 인덱스 번호 (child node’s index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node’s index) = 부모 노드 인덱스 번호 (parent node’s index) * 2 + 1
class heap:
# ... init
# insert 안에서 사용할 move_up 함수를 먼저 작성한다.
# 입력받은 노드와 부모 노드의 자리를 바꿔야 하면 true를 그렇지 않으면 false를 반환한다.
def move_up(self, inserted_idx):
# 입력받은 노드가 root 노드이면
if inserted_idx <= 1:
# false를 반환한다.
return false
# parent 노드의 인덱스는 입력받은 노드의 인덱스를 2로 나눈 몫 값이다.
parent_idx = inserted_idx // 2
# 입력받은 노드의 인덱스가 parent 노드의 인덱스보다 크면
if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
# true를 반환한다.
return true
# 아니면
else:
# false를 반환한다.
return false
def insert(self, data):
if len(self.heap_array) == 0:
self.heap_array.append(none)
self.heap_array.append(data)
return true
self.heap_array.append(data)
# 여기서부터 작성
# 우선 현재 생성한 노드의 인덱스 번호를 구한다.
inserted_idx = len(self.heap_array) - 1
# move_up의 반환 값이 true인 동안
while self.move_up(inserted_idx):
# parent 노드의 인덱스를 먼저 구하고
parent_idx = inserted_idx // 2
# 삽입한 노드와 parent 노드의 자리를 바꾼다.
self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
# 자리를 바꿨으니 인덱스값도 parent의 인덱스였던 값으로 바꾼다.
inserted_idx = parent_idx
return true
# 테스트
# root 노드 생성
heap = heap(15)
# 위의 예시대로 값을 넣는다.
heap.insert(10)
heap.insert(8)
heap.insert(5)
heap.insert(4)
heap.insert(20)
heap.heap_array # [none, 20, 10, 15, 5, 4, 8]
힙에 데이터 삭제 구현 (max heap 예)
- 힙 클래스 구현 4 - delete 1
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 중간 노드를 삭제하는 일은 거의 없다.
- 힙의 용도는 최댓값 또는 최솟값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
class heap:
# ... init, move_up, insert
def pop(self):
# heap_array에 실질적인 노드가 없는 경우
# 인덱스 0의 값은 none이기 때문에 길이가 1 이하이다.
if len(self.heap_array) <= 1:
return none
# 보통 pop에서는 반환하는 데이터를 지우는 과정도 있지만
# 아래서 자식 노드를 root로 가져오면서 덮어쓰면 되기 때문에 별도로 지우지 않는다.
returned_data = self.heap_array[1]
return returned_data
- 힙 클래스 구현 4 - delete 2
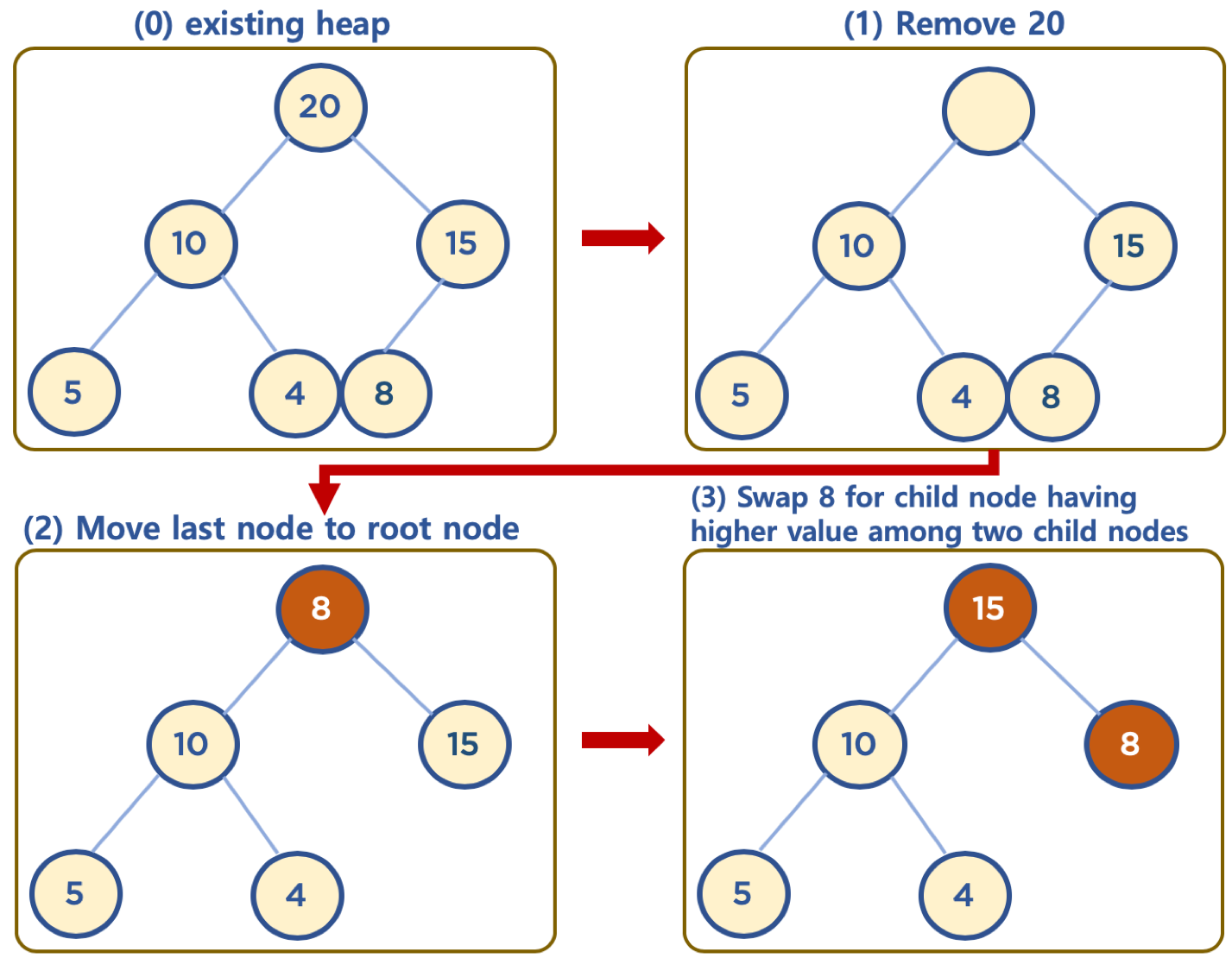
- 상단의 데이터 삭제 시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드)를 root 노드로 이동
- root 노드의 값이 child node보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
class heap:
# ... init, move_up, insert
# pop 안에서 사용할 move_down 함수를 먼저 작성한다.
# 입력받은 노드와 자식 노드의 자리를 바꿔야 하면 true를 그렇지 않으면 false를 반환한다.
def move_down(self, popped_idx):
# 자식 노드의 인덱스를 구한다.
left_child_popped_idx = popped_idx * 2
right_child_popped_idx = popped_idx * 2 + 1
# case 1: 왼쪽 자식 노드도 없을 때
# 입력받은 노드의 왼쪽 노드의 인덱스가 heap_array 크기보다 크거나 같으면
# 인덱스 0에 의미 없는 원소가 하나 포함되어있기 때문에 크기가 같은 경우도 포함된다.
if left_child_popped_idx >= len(self.heap_array):
# 바꿀 게 없는 경우이기 때문에 그냥 false를 반환하면 된다.
return false
# case 2: 오른쪽 자식 노드만 없을 때
# 위의 조건에서 왼쪽 노드의 인덱스 값만 오른쪽 노드의 인덱스 값으로 바꿔주면 된다.
elif right_child_popped_idx >= len(self.heap_array):
# 입력받은 노드의 값이 해당 노드의 왼쪽 노드의 값보다 작으면
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
# true를 반환한다.
return true
else:
return false
# case 3: 왼쪽, 오른쪽 자식 노드 모두 있을 때
# 두 자식 노드 중 더 큰 노드와 자리를 바꿔야 한다.
else:
# 왼쪽 노드의 값이 오른쪽 노드의 값보다 크고
if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
# 그 값(왼쪽 노드의 값)이 입력받은 노드의 값보다 크면
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
# true를 반환한다.
return true
else:
return false
# 오른쪽 노드의 값이 왼쪽 노드의 값보다 크고
else:
# 그 값(오른쪽 노드의 값)이 입력받은 노드의 값보다 크면
if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
# true를 반환한다.
return true
else:
return false
def pop(self):
if len(self.heap_array) <= 1:
return none
returned_data = self.heap_array[1]
# 여기서부터 작성
# root(인덱스 1번)에 마지막(인덱스 -1번) 값을 넣는다.
self.heap_array[1] = self.heap_array[-1]
# 마지막 값은 필요 없으므로 지워준다.
del self.heap_array[-1]
# move_down 함수의 출발은 항상 root 이므로
# move_down의 인자로 전달할 popped_idx를 1로 지정한다.
popped_idx = 1
# move_down인 true인 동안
while self.move_down(popped_idx):
# 두 자식 노드의 인덱스 값을 계산하고
left_child_popped_idx = popped_idx * 2
right_child_popped_idx = popped_idx * 2 + 1
# 왼쪽 자식 노드가 없을 때는 무조건 false가 반환되므로 고려할 필요가 없다.
# case 2: 오른쪽 자식 노드만 없을 때
if right_child_popped_idx >= len(self.heap_array):
# 현재 값보다 왼쪽 자식 노드의 값이 더 크면
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
# 두 노드의 자리를 바꾼다.
self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx]
popped_idx = left_child_popped_idx
# case 3: 왼쪽, 오른쪽 자식 노드 모두 있을 때
else:
# 왼쪽 노드의 값이 오른쪽 노드보다 크고
if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
# 왼쪽 노드의 값이 현재 값보다 크면
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
# 두 노드의 자리를 바꾼다.
self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx]
# 현재 인덱스를 왼쪽 노드의 인덱스로 바꾼다. (왼쪽 노드로 이동한다)
popped_idx = left_child_popped_idx
# 오른쪽 노드의 값이 오른쪽 노드보다 크고
else:
# 오른쪽 노드의 값이 현재 값보다 크면
if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
# 두 노드의 자리를 바꾼다.
self.heap_array[popped_idx], self.heap_array[right_child_popped_idx] = self.heap_array[right_child_popped_idx], self.heap_array[popped_idx]
# 현재 인덱스를 오른쪽 노드의 인덱스로 바꾼다. (오른쪽 노드로 이동한다)
popped_idx = right_child_popped_idx
return returned_data
# 테스트
# 우선 heap_array를 구성한다.
heap = heap(15)
heap.insert(10)
heap.insert(8)
heap.insert(5)
heap.insert(4)
heap.insert(20)
# 출력해서 확인한다.
heap.heap_array # [none, 20, 10, 15, 5, 4, 8]
# pop을 하면 root의 20이 추출된다.
heap.pop() # 20
# 출력하면 재구성이 잘 된 것을 확인할 수 있다.
heap.heap_array # [none, 15, 10, 8, 5, 4]
5. 힙 (heap) 시간 복잡도
- depth (트리의 높이)를 h라고 표기한다면,
- n개의 노드를 가지는 heap에 데이터 삽입 또는 삭제 시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 $h=\log 2n$ 에 가까우므로, 시간 복잡도는 $o(\log n)$
- 참고: 빅오 표기법에서 $\log n$ 에서의 log의 밑은 10이 아니라, 2입니다.
- 한번 실행 시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행 시간을 단축할 수 있다는 것을 의미함